Nicolas Saintier
- Assistant-professor in the Mathematics Departement of the University of Buenos-Aires (UBA-Argentina),
- Under contract with the CONICET as assistant researcher.
To contact me
- nsaintie-at-dm.uba.ar
- Departamento de Matemática, Facultad de Ciencias Exactas y Naturales (1428) Pabellón I - Ciudad Universitaria, Buenos Aires - ARGENTINA
Curriculum espanol,
francais
english
NEWS
- 18/04/2022: With A.S. Ackleh and A. Zhang we submitted the paper "A multiple-strain pathogen model with diffusion on the space of Radon measures"
We propose a SIS model with spatial diffusion where the disease has a multiple strains.
To unify discrete and continuous strain distribution, we model the strain distribution with a meaure.
We obtain the well-posedness of the resulting system and study the long-time behaviour of the solution obtaining that
only the fittest strain survives.
- March 2022 - June 2002: I am visiting Prof. Marino Belloni at the University of Parma (Italy).
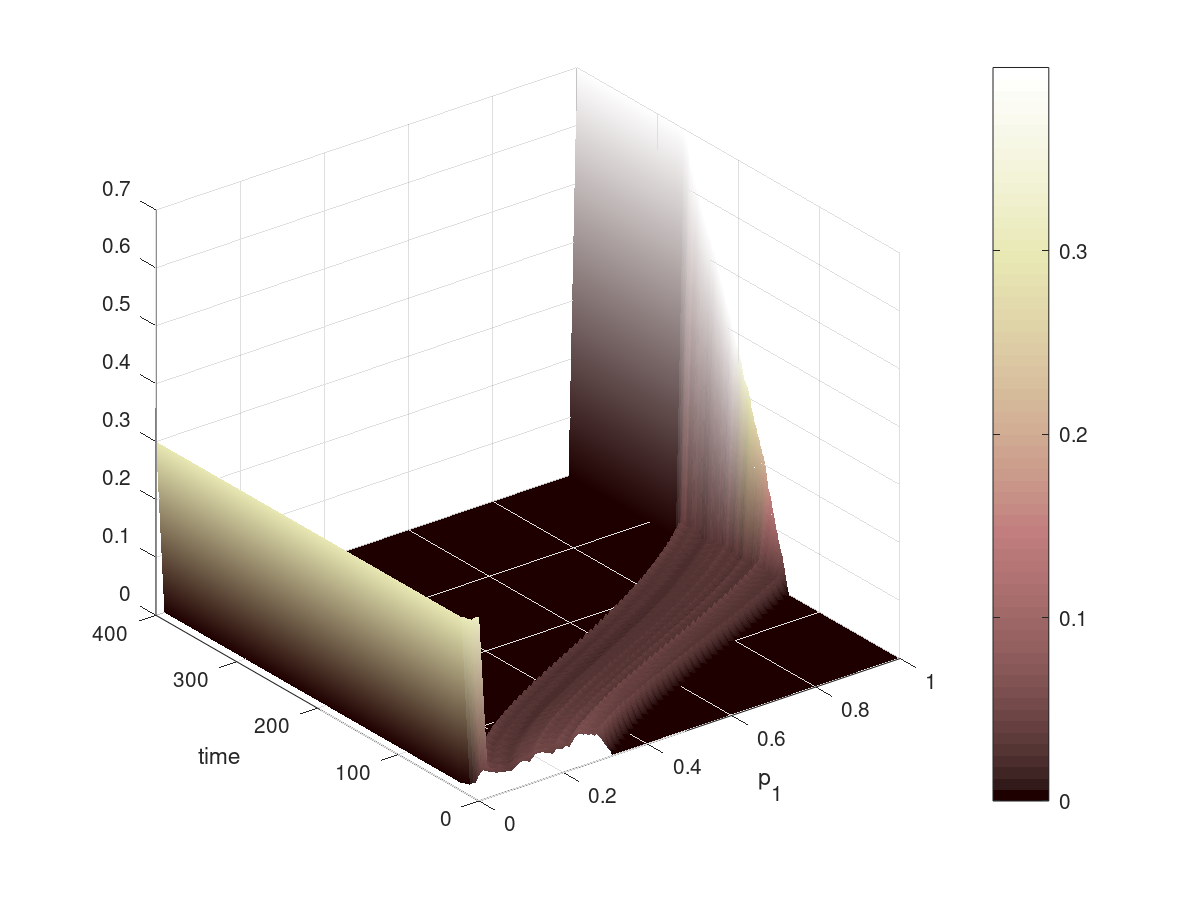
- December 2021 and January 2022: with J.P. Pinasco, M. Kind and J. Marenco, motivated by renewable energy auctions,
we studied a simplified model of auctions for a large number of bidders
taking place in several rounds. Bidders can learn from one round to the next adjusting slightly raising or lowering their bid according
to their result in the round. We numerically observed a phase transition when varying the competition level. To explain it, we deduce an equation
(1st order non-linear) for the distribution of bids and qualitatively study its long-time behaviour. Though simple, this model can reprouce fairly well
the outcomes of real auctions.
- 18/12/20: With A.S. Ackleh and R. Lyons, we submitted the paper "Structured Coagulation-Fragmentation Equation in the Space of Radon Measures:
Unifying Discrete and Continuous Models". We study the coagulation-fragmentation in the space of measure. We prove well-posedness
of the equation and devise a semi-discrete numerical scheme which preserve mass. In view of the various numerical experiments
we present, this scheme seems to be of order 2. We also give a regularity result.
Here is the preprint.
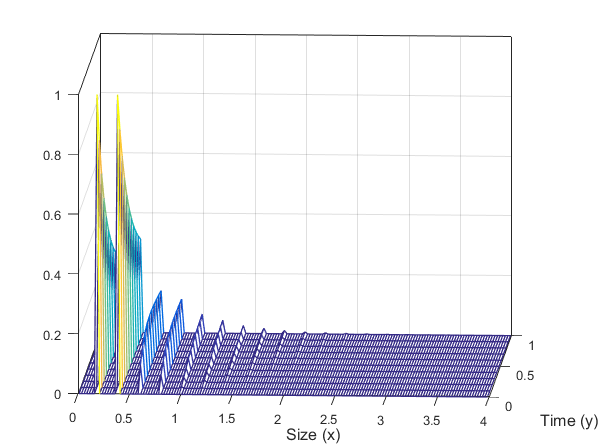
- 12/10/20: The paper "Evolutionary game theory in mixed strategies: from microscopic interactions to kinetic equations" has been accepted
in Kinetic and Related Models. We studied a large population of agents
interacting by playing a game (a 2-players symmetric zero-sum game).
After each game, the two participants myopically update their mixed strategy profile slightly raising the probability of playing
the winning strategy and decreasing the loosing one. In the mean-field limit the distribution of
mixed strategies in the population evolves according to a first order equation.
Interestingly, the vector field driving this equation is very much related to the vector field of the replicator
equation, central in evolutionnary game theory. We explore further this connection.
For instance in the case of a two strategies game here is the evolution of the probability of playing the
dominant strategy:
 Here is the preprint.
Here is the preprint.
- 23/08/20: Sometime ago Juan Pablo Pinasco had the idea to couple opinion formation models like those we are studying
with epidemiological models (like SIS, SIR and all the available variant) in a way that both dynamics interact:
the status of an individual (healthy, ill ...) influence his opinion about hygiene measures (like vaccination for instance
or respect of social distance), and in return his hygiene effort level affects the rate of contagion.
Lockdown and hygiene measure due to coronavirus and its social acceptance have clearly a great impact on
propagation of the disease.
We eventually submitted today the first paper in this line with Carlo Giambiagi Ferrari.
Here is the
preprint.
We have a few more in preparation following the same idea.
- 02/08/20: With Mayte Perez-Llanos and Juan Pablo Pinasco, we are pursuing our effort in modelling opinion
formation processes. We studied the impact of on the dynamic of the attractiveness or unatractaviness of certain opinion.
We already explored numerically this idea in our Physica A paper
"Opinion attractiveness and its effect in opinion formation models".
We only provided heuristic argument to write down the explicit expression of the consensus opinion, in case consensus occur.
In this new paper we rigurously proved convergence results with estimate of the convergence rate.
- 15/06/20: We finally submitted the last paper from Mauro Rodriguez Cartabia PhD thesis. It deals with
with a population of interacting agents in the mean-field case with a general delay.
We study the limit of this system as the number of agents goes to infinity and obtain a
delay differential equation with random initial condition.
We prove its well-posedness.
Here is the preprint.
- 05/06/20: Our paper with J.P. Pinasco and F. Vazquez ""A model for the competition between political mono-polarization and
bi-polarization"" has been accepted in Chaos: An Interdisciplinary Journal of Nonlinear Science.
Here is the preprint.
- 07/05/20: The country-wide distrbuted paper "La Nacion" published
a note
about our Physical Review E paper
"The role of voting intention in public opinion polarization" written with J.P. Pinasco and F. Vazquez.
- 17/02/20: With Juan Pablo Pinasco and Mauro Rodriguez-Cartabia, we studied a large population of agents
interacting by playing a game (a 2-players symmetric zero-sum game).
After each game, the two participants myopically update their mixed strategy profile slightly raising the probability of playing
the winning strategy and decreasing the loosing one. In the mean-field limit the distribution of
mixed strategies in the population evolves according to a first order equation.
Interestingly, the vector field driving this equation is very much related to the vector field of the replicator
equation, central in evolutionnary game theory. We explore further this connection.
For instance in the case of a two strategies game here is the evolution of the probability of playing the
dominant strategy:
 Here is the preprint.
Here is the preprint.
- 17/02/20: With Federico Vazquez and Juan Pablo Pinasco we keep on studying
models of opinion formation. We introduced a non-linear version of our recent PRE paper
and show that a stable bi-polarization state is possible without any hard-wired homophily nor explicit self-reinforcement.
Here is the preprint.
- 18/12/19: Physical Review E accepted our paper "The role of voting intention in public opinion polarization" where we consider a simple
stochastic mechanism yielding polarization without assuming negative influence or homophily.
It is a team work with Federico Vazquez
and Juan Pablo Pinasco.
Here is the preprint.
- 8/11/19: my paper with Laurent Veron "Nonlinear elliptic equations with measure valued absorption potentials"
is accepted in "Annali della Scuola Normale Superiore di Pisa, Classe di Scienze".
Here is the preprint.
- 4/11/19: my paper
"Finite difference schemes for a structured population model in the space of
measures"
with Azmy Ackleh
and Rainey Lyons is published in
Mathematical Biosciences and Engineering.
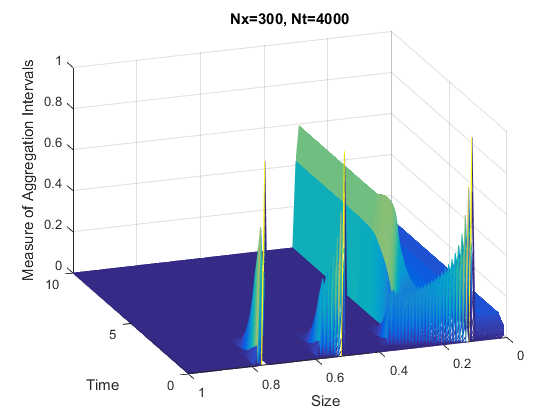
We propose a fast scheme to solve numerically transport equations modelling structured population
in the framework of measure-valued functions.
Here is an illustration of our algorithm:
- 21/10/19: my paper
"Sensitivity equations for measure-valued solutions to transport equations"
with Azmy Ackleh
and Jakub Skrzeczkowski
is published in
Mathematical Biosciences and Engineering.

 Here is the preprint.
Here is the preprint.
 Here is the preprint.
Here is the preprint.
