- clase 1 (26/3)
Presentación de la materia. La función zeta de Riemann. La serie
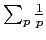 diverge. Funciones aritméticas: ejemplos
(Las funciones d(n) y
diverge. Funciones aritméticas: ejemplos
(Las funciones d(n) y 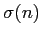 ,
, 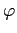 de Euler y
de Euler y 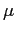 de Möbius.
La convolución de Dirichlet. La fórmula de inversión de Möbius.
de Möbius.
La convolución de Dirichlet. La fórmula de inversión de Möbius.
- clase 2 (31/3)
Propiedades de
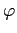 .
Funciones multiplicativas y completamente multiplicativas
Series de Dirichlet: semiplano de convergencia absoluta. Teorema de
unicidad. Relación de la convolución de Dirichlet con el producto de series de
Dirichlet.
.
Funciones multiplicativas y completamente multiplicativas
Series de Dirichlet: semiplano de convergencia absoluta. Teorema de
unicidad. Relación de la convolución de Dirichlet con el producto de series de
Dirichlet.
- clase 3 (7/4)
Ejermplos de funciones generatrices. Derivada de una serie de Dirichlet. La
función de Mangoldt. Productos infinitos. Productos de Euler.
- clase 4 (14/4)
Medias de funciones aritméticas: fórmula de sumación de Euler. Fórmulas
asintóticas elementales. Prolongación analítica de la función zeta a
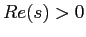 (salvo un polo simple en
(salvo un polo simple en  ). Método de la hipérbola de
Dirichlet. Orden medio de
). Método de la hipérbola de
Dirichlet. Orden medio de 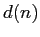 y
y 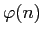 .
.
- clase 5 (16/4
Versión más refinada del método de la hipérbola de Dirichlet. Funciones de
Chebyshev, y métodos elementales para estudiar la distribución de los
números primos.
- clase 6 (21/4)
Equivalencias del teorema de los números primos. Otras consecuencias de las
cotas de Chebyshev. Fórmula de sumación de Abel. Teorema de Mertens.
Aplicación a la cantidad de factores primos de un número.
- clase 7 (23/4)
(apunte parcial): Otro teorema de Mertens. La no anulación de la función
zeta en la recta
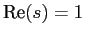 .
.
- clases 8 y 9 (28/4 y 30/4): Expusimos la prueba de D. J. Newman del
teorema de los números primos siguiendo las
notas de R. Ash y R. Novinger
- clase 10 (5/5): Aplicaciones del teorema de los números primos
al estudio de las crecimiento de las funciones d(n)
y
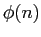 [Apostol, Capítulo sección 13.10 y sección 13.11
(teoremas 13.12 y 13.14)].
[Apostol, Capítulo sección 13.10 y sección 13.11
(teoremas 13.12 y 13.14)].
- clase 11 (12/5/2009)
(7/5/2009) Teorema de Fermat-Euler,
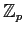 es cíclico,
restos y no-restos cuadráticos, símbolo de Legendre, aplicación del
teorema chino del resto a la estructura de
es cíclico,
restos y no-restos cuadráticos, símbolo de Legendre, aplicación del
teorema chino del resto a la estructura de
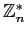 .
.
- clase 12 (12/5/2009)
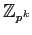 es cíclico si
es cíclico si 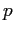 es un primo impar. Caracteres
de grupos abelianos finitos. Caracteres de Dirichlet.
es un primo impar. Caracteres
de grupos abelianos finitos. Caracteres de Dirichlet.
- clase 13 (14/5): Más sobre caracteres de Dirichlet: relaciones de
ortogonalidad. L-series. Producto de Euler. Formulas para 1/L y L'/L
- clase 14 (19/5): Estructura de
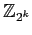 (Apostol, teoremas 10.3 y
10.11). Más sobre caracteres y L-series.
(Apostol, teoremas 10.3 y
10.11). Más sobre caracteres y L-series.
- clase 15 (21/5): La no anulación de las L-series de Drichlet
en la recta
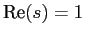 . (Para los caracteres reales y
. (Para los caracteres reales y  utilizamos
el argumento de Apostol, teorema 6.20).
utilizamos
el argumento de Apostol, teorema 6.20).
- clase 16 (26/5): Prueba del teorema de Dirichlet sobre la
infinitud de los primos en progresiones aritméticas (ver por ejemplo
C. Ivorra, Funciones de Variable compleja (con aplicaciones a la teoría analítica de
números)., teorema 7.34)
, y del teorema de los primos para progresiones aritmeticas
(ver el apunte parcial de la clase
o el artículo de I. Soprounov A short proof of the Prime Number Theorem
for Arithmetic Progressions.
)
- clase 17 (28/5): Sumas de Gauss asociadas a los caracteres de
Dirichlet. Caracteres primitivos.
- clase 18 (2/6) números y polinomios de Bermoulli.
Aplicaciones: fórmula de Euler-Maclaurin. Valores de la función zeta en
los enteros pares.
- clase 19: (4/6) La función theta de Jacobi. La identidad modular:
vimos una prueba basada en el análisis complejo
debida a W. Cowenberg ). Alternativamente la identidad modular puede demostrarse
utilizando análisis de Fourier, ver por ejemplo las
(notas de Been Green).
- clase 20 (9/6): La función Gama. Su desarrollo en producto infinito.
- clase 21 (11/6): La ecuación funcional para la zeta de Riemann. Productos
infinitos: teorema de Weierstrass sobre factorización de las funciones
enteras.
- clases 22 y 23 (16/6 y 23/6): Funciones enteras de orden finito.
Teorema de Hadamard sobre su factorización en producto infinito.
- clases 24 y 25 (23/6 y 25/6): Aplicación a la función zeta: Desarrollo
en fracciones simples para su derivada logarítimica. Región clásica libre de
ceros.
- clase 26 (30/6): La fórmula de Perron. Teorema de los números primos
con error.
- clase 27 (2/6): Breve introducción a la teoría algebraica de números,
y sus conexiones con la teoría analítica (la función zeta de Dedekind).
2009-07-04