K-theory school

• The Farrell-Jones Conjecture. Arthur Bartels (Münster, Germany)

The Farrell-Jones Conjecture gives a structural picture of the K- and L-theory of group rings. It has many applications to the classification of manifolds and questions about group rings. Proofs of instances of this conjecture often combine methods from algebraic topology and K-theory with methods from geometric group theory. In this course we will explain the conjecture, its applications and methods of proof.

• Combinatorial aspects of algebraic K-theory, Inna Zakharevich (Cornell, USA)

In this course we discuss the combinatorial aspects of K-theory. We begin with a discussion of the Barratt-Priddy-Quillen Theorem and its connection between the topology of the sphere spectrum and the combinatorics of the symmetric groups. From this, we proceed to the construction of Waldhausen A-theory, and discuss several of its applications. Throughout the discussion we emphazise the connections between the combinatorial construction of K-theory and its topological implications.

• Algebraic K-theory for rings of functional analytic type. Andreas Thom (Dresden, Germany)

I want to review some recent results on the comparison of algebraic and topological K-theory for topological  rings, such as operator ideals or rings of continuous functions on a topological space. A main theme here is automatic homoty invariance of a certain algebraically defined functors. I will mention Karoubi's Conjecture (as proved by Mariusz Wodzicki) and a recent result on homotopy invariance of negative algebraic K-theory of the ring of continuous functions on a topological space.

• Introduction to algebraic K-theory  Charles Weibel (New Brunswick, USA)

The first lecture will discuss all the different constructions of K_0. The second lecture will describe the constructions of higher K-theory and some basic structural results, such as transfer maps. The third lecture will cover some of the basic exact sequences in K-theory. The final lecture will survey computations for regular

rings and smooth varieties, using motivic cohomology and etale cohomology.

.

• The classification of AF C*-algebras. Beatriz Abadie (UdelaR, Montevideo,Uruguay)

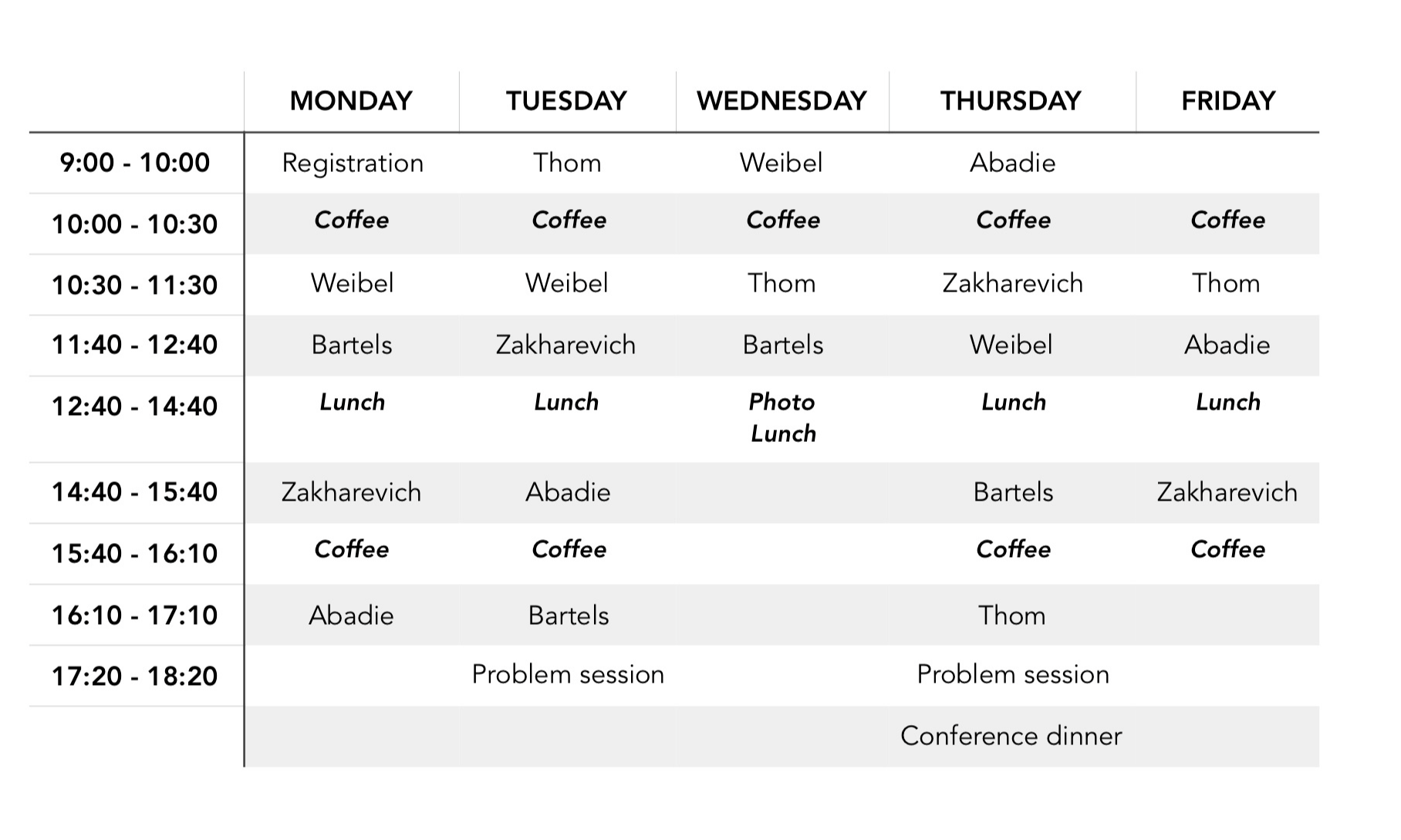
A C*-algebra is approximately finite-dimensional (AF) if it is the inductive limit of a sequence of finite-dimensional C*-algebras. We will construct the dimension group of a unital AF C*-algebra by providing its K_0-group with a structure of scaled ordered group. We will then discuss Elliott's theorem, which shows that two unital AF C*-algebras are isomorphic if and only if their dimension groups are isomorphic as ordered groups.