- Funciones aritméticas: ejemplos (las funciones d(n) y
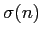 ,
, 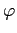 de Euler y
de Euler y 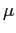 de Möbius).
La convolución de Dirichlet. La fórmula de inversión de Moëbius. Medias de funciones aritméticas. Fórmulas de sumación
de Euler y de Abel.
de Möbius).
La convolución de Dirichlet. La fórmula de inversión de Moëbius. Medias de funciones aritméticas. Fórmulas de sumación
de Euler y de Abel.
- Métodos elementales para estudiar la distribución de los números primos:
Funciones de Chevishev. Distintas formas equivalentes del teorema de los
números primos.
- Funciones generatrices. Teoría aditiva: particiones. Teoría
multiplicativa: Series de Dirichlet. Productos de Euler. Ejemplos.
- Algunos temas de variable compleja (necesarios para estudiar la función
zeta y las L-series de Dirichlet): Funciones enteras de orden finito.
Fórmula de Jensen. Teorema de factorización de Hadamard. Función Gama.
- La función zeta de Riemann. Su prolongación al plano complejo como
función meromorfa. Ecuación funcional. Región clásica libre de ceros de la
función zeta y demostración del teorema de los números primos.
- Relación entre la distribución de los ceros de la función zeta y la
distribución de los números primos (``fórmulas explícitas''). Teorema de los
números primos con error. Hipótesis de Riemann.
- Caracteres de grupos abelianos finitos. Los caracteres de Dirichlet y sus
sumas de Gauss. L-Series de Dirichlet: prolongación analítica y ecuación
funcional. Teorema de Dirichlet sobre la infinitud de los primos
en progresiones aritméticas.
2009-07-04