Horarios:
Martes y Jueves de 14 a 17.
Aula 7 Pab. I
Finales:
Vaya hasta el final de la página para ver una lista de papers posibles (sigo agregando).
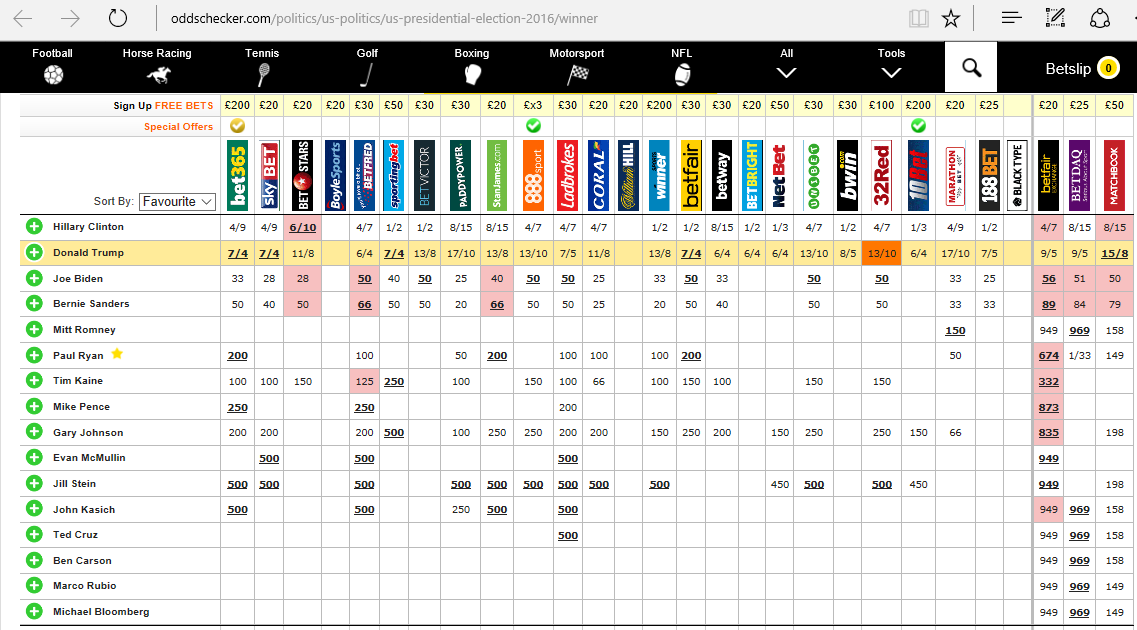
Utimos números de las apuestas:
(Abrir para ver más grande. El cierre de apuestas lo pone ganador a Trump...)
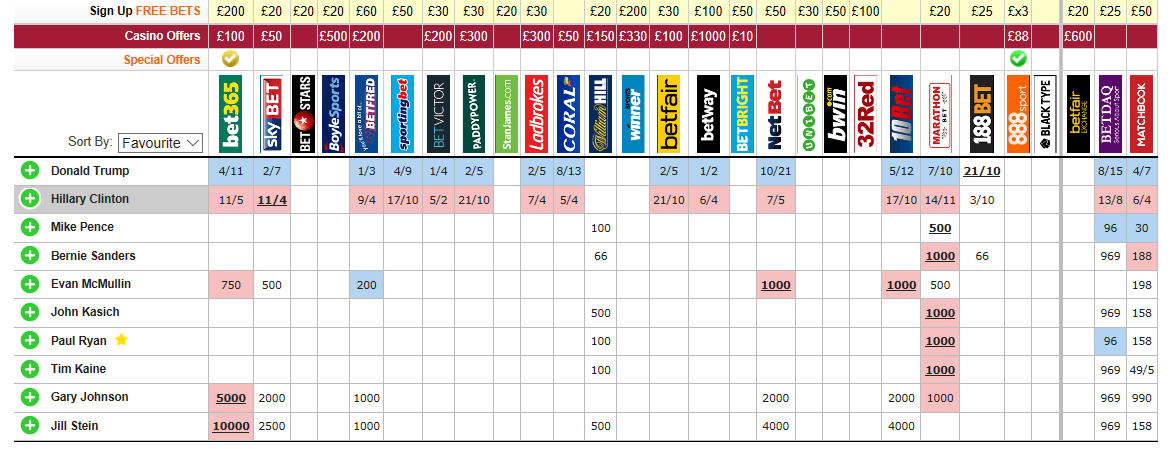
16/xi:
Vamos a seguir con modelos de interacción grupal: sincronización.
Links:
1 - 3/xi:
Vamos a ver modelos de interacción grupal: Hegselmann-Krause, sincronización, Cucker-Smaile y flocking/swarming.
Links:
Martes 25-x:
Modelos de crimen UCLA y Berestycki-Nadal.
Ver charla de Berestycki sobre los distintos modelos (archivo)
Undécima Semana:
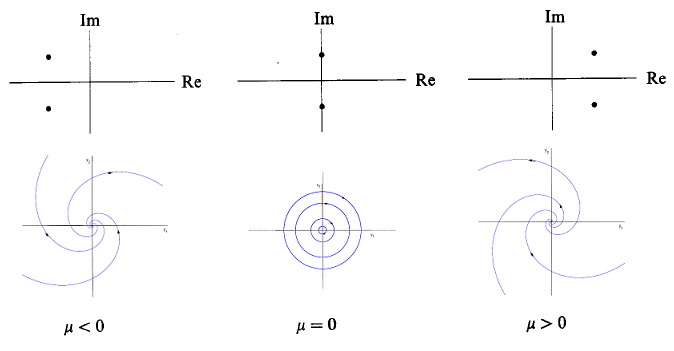
Epidemias: SI, SIS, SIR + difusión.
¿Qué son estos gráficos? (abrir para ver más grandes)
Décima Semana:
El martes vimos el modelo de segregación de Schelling (pdf aquí), y les recomiendo leer:
TC Schelling, Some fun, thirty-five years ago, Handbook of Computational Economics, 2006 Elsevier (ver aquí).
Vamos a ver los modelos de forest fire (ver aquí y aquí) y avalanchas en sand piles. Algunas cosas interesantes relacionadas
C.J. Rhodes, R.M. Anderson, Power laws governing epidemics in isolated populations, Nature (1996) (ver paper aquí)
D.H. Zanette, S.C. Manrubia Vertical transmission of culture and the distribution of family names, Physica A: Statistical Mechanics and its Applications, 295 (2001) (ver paper aquí)

Octava y novena semana:
Novedades: el survey de Esteban Moro, The Minority Game: an introductory guide, es una de las mejores cosas que pueden leer para empezar con El Farol Bar y el Minority Game (artículo disponible aquí)
Para escuchar mientras lo leen, Should I stay or should I go?
Esta semana comenzamos con modelos basados en autómatas. Una buena intro al tema es la siguiente:
Martin Gardner, The fantastic combinations of John Conway's new solitaire game "life", Scientific American 223, Oct '70
El material más teórico, y algunos de los modelos, los voy a extraer de distintos artículos y libros:
Séptima (?) semana:
Veremos modelos bayesianos para la formación de precios futuros, formación de precios y mercados, y distribución de riqueza (sin interacciones entre agentes).
Cont y Bouchaud, Herd behavior and aggregate fluctuations, Macroeconomic dynamics 4.02 (2000): 170-196. (artículo disponible aquí)
El modelo de formación de sociedades y el análisis teórico del paper anterior se pueden ver en
Abrir para ver más grande:
Quinta y sexta semana:
Modelos de opinión. Slanina-Lavicka y Ochrombel. Ecuaciones de transporte: existencia, unicidad, estabilidad.
Asch "social pressure" experiments:
--------------------------------------------------------------------
Cuarta semana:
Bajen y miren este pdf de V. Blondel
--------------------------------------------------------------------
Tercera semana:

----------------------------------------------------------------
Segunda semana: (abrir para ver más grandes)
-----------------------------------------------------------------
Primera semana: jpp-ssc1.pdf
-----------------------------------------------------------------
FINALES: Gente que vale la pena leer:
Andrea Baronchelli.
Alain Barrat .
Andreas Flache .
Dirk Helbing.
Vittorio Loreto.
Yamir Moreno.
Clément Mouhot.
Lorenzo Pareschi .
Romualdo Pastor-Satorras.
Matjaz Perc.
Maxi San Miguel.
Frantisek Slanina.
Attila Szolnoki.
Giuseppe Toscani .
Federico Vazquez.
Alessandro Vespignani.
Tamás Vicsek .
Damián Zanette.
Algunos papers:
Evolutionary instability of zero-determinant strategies demonstrates that winning is not everything. Nature communications 4 (2013).
Modeling Warfare in Social Animals: A "Chemical" Approach
Alisa Santarlasci, Gianluca Martelloni, Filippo Frizzi, Giacomo Santini, Franco Bagnoli
The aim of our study is to describe the dynamics of ant battles, with reference to laboratory experiments, by means of a chemical stochastic model. We focus on ants behavior as an interesting topic in order to predict the ecological evolution of invasive species and their spreading. In our work we want to describe the interactions between two groups of different ant species with different war strategies. Our model considers the single ant individuals and fighting groups in a way similar to atoms and molecules, respectively, considering that ant fighting groups remain stable for a relative long time. Starting from a system of differential non-linear equations (DE), derived from the chemical reactions, we obtain a mean field description of the system. The DE approach is valid when the number of individuals of each species is large in the considered unit, while we consider battles of at most 10 vs. 10 individuals, due to the difficulties in following the individual behavior in a large assembly. Therefore, we also adapt a Gillespie algorithm to reproduce the fluctuations around the mean field. The DE scheme is exploited to characterize the stochastic model. The set of parameters of chemical equations, obtained using a minimization algorithm, are used by the Gillespie algorithm to generate the stochastic trajectories. We then fit the stochastic paths with the DE, in order to analyze the variability of the parameters and their variance. Finally, we estimate the goodness of the applied methodology and we confirm that the stochastic approach must be considered for a correct description of the ant fighting dynamics. With respect to other war models, our chemical one considers all phases of the battle and not only casualties. Thus, we can count on more experimental data, but we also have more parameters to fit. In any case, our model allows a much more detailed description of the fights.
A three-state kinetic agent-based model to analyze tax evasion dynamics
Nuno Crokidakis
In this work we study the problem of tax evasion on a fully-connected population. For this purpose, we consider that the agents may be in three different states, namely honest tax payers, tax evaders and undecided, that are individuals in an intermediate class among honests and evaders. Every individual can change his/her state following a kinetic exchange opinion dynamics, where the agents interact by pairs with competitive negative (with probability q) and positive (with probability 1-q) couplings, representing agreement/disagreement between pairs of agents. In addition, we consider the punishment rules of the Zaklan econophysics model, for which there is a probability pa of an audit each agent is subject to in every period and a length of time k detected tax evaders remain honest. Our results suggest that below the critical point qc=1/4 of the opinion dynamics the compliance is high, and the punishment rules have a small effect in the population. On the other hand, for q>qc the tax evasion can be considerably reduced by the enforcement mechanism. We also discuss the impact of the presence of the undecided agents in the evolution of the system.
Committed activists and the reshaping of status-quo social consensus
Dina Mistry, Qian Zhang, Nicola Perra, Andrea Baronchelli
The role of committed minorities in shaping public opinion has been recently addressed with the help of multi-agent models. However, previous studies focused on homogeneous populations where zealots stand out only for their stubbornness. Here, we consider the more general case in which individuals are characterized by different propensities to communicate. In particular, we correlate commitment with a higher tendency to push an opinion, acknowledging the fact that individuals with unwavering dedication to a cause are also more active in their attempts to promote their message. We show that these \textit{activists} are not only more efficient in spreading their message but that their efforts require an order of magnitude fewer individuals than a randomly selected committed minority to bring the population over to a new consensus. Finally, we address the role of communities, showing that partisan divisions in the society can make it harder for committed individuals to flip the status-quo social consensus.
Kinetics of Social Contagion
Zhongyuan Ruan, Gerardo Iniguez, Marton Karsai, Janos Kertesz
Diffusion of information, behavioral patterns or innovations follows diverse pathways depending on a number of conditions, including the structure of the underlying social network, the sensitivity to peer pressure and the influence of media. Here we study analytically and by simulations a general model that incorporates threshold mechanism capturing sensitivity to peer pressure, the effect of `immune' nodes who never adopt, and a perpetual flow of external information. While any constant, non-zero rate of dynamically-introduced spontaneous adopters leads to global spreading, the kinetics by which the asymptotic state is approached shows rich behavior. In particular we find that, as a function of the immune node density, there is a transition from fast to slow spreading governed by entirely different mechanisms. This transition happens below the percolation threshold of network fragmentation, and has its origin in the competition between cascading behavior induced by adopters and blocking due to immune nodes. This change is accompanied by a percolation transition of the induced clusters.
Proposal of a risk model for vehicular traffic: A Boltzmann-type kinetic approach
Paolo Freguglia, Andrea Tosin
This paper deals with a Boltzmann-type kinetic model describing the interplay between vehicle dynamics and safety aspects in vehicular traffic. Sticking to the idea that the macroscopic characteristics of traffic flow, including the distribution of the driving risk along a road, are ultimately generated by one-to-one interactions among drivers, the model links the personal (i.e., individual) risk to the changes of speeds of single vehicles and implements a probabilistic description of such microscopic interactions in a Boltzmann-type collisional operator. By means of suitable statistical moments of the kinetic distribution function, it is finally possible to recover macroscopic relationships between the average risk and the road congestion, which show an interesting and reasonable correlation with the well-known free and congested phases of the flow of vehicles.
Balancer effects in opinion dynamics
Taksu Cheon, Jun Morimoto
We introduce a novel type of contrarian agent, the balancer, to Galam model of opinion dynamics, in order to account for the existence of social skepticism over one-sidedness. We find that the inclusion of balancers, along with majoritarian floaters and single-sided inflexibles, brings about the emergence of a critical point on parametric pl
Spatial Boundaries and the Local Context of Residential Segregation
Elizabeth Roberto
Spatial boundaries are a defining feature of a city's social and spatial organization. Rivers, highways, and train tracks create excess distance between nearby locations and often mark social separation -- they become dividing lines that are well known to residents. Qualitative studies are rich with insight about the local significance of boundaries, but they have been largely ignored in the quantitative segregation literature. I advance existing scholarship by integrating spatial boundaries into the way we measure residential segregation for city populations. I introduce a new method that measures the proximity of residential locations and the reach of local environments around each location using road distance. This is more realistic than straight line ("as the crow flies") distance, because it captures the connectivity of roads and the distance imposed by physical boundaries. I measure segregation using the Divergence Index, which evaluates how surprising the composition of each local environment is given the overall population. I use this new approach to examine how spatial boundaries structure patterns of racial and ethnic residential segregation in U.S. cities. Results reveal the salience of city boundaries in structuring segregation patterns in Detroit, and how the presence of physical boundaries affects the composition of local environments in Manhattan. Further, the experience of segregation is highly unequal within cities such as St. Louis. Some residents live in completely segregated environments, while others live in areas that are a microcosm of the city's diverse population. This research bridges qualitative insight on the local experience of segregation and how we measure segregation for city populations. My emphasis on spatial boundaries and local context reframes our understanding of segregation, and offers deeper insight into even the most studied U.S. cities.
A hierarchical kinetic theory of birth, death, and fission in age-structured interacting populations
Tom Chou, Chris D Greenman
We study mathematical models describing the evolution of stochastic age-structured populations. After reviewing existing approaches, we present a full kinetic framework for age-structured interacting populations undergoing birth, death and fission processes, in spatially dependent environments. We define the complete probability density for the population-size-age-chart and find results under specific conditions. Connections with more classical models are also explicitly derived. In particular, we show that factorial moments for non-interacting processes are described by a natural generalization of the McKendrick-von Foerster equation, which describes mean-field deterministic behaviour. Our approach utilizes mixed type, multi-dimensional probability distributions similar to those employed in the study of gas kinetics, with terms that satisfy BBGKY-like equation hierarchies.
When is a bottleneck a bottleneck?
Andreas Schadschneider, Johannes Schmidt, Vladislav Popkov
Bottlenecks, i.e. local reductions of capacity, are one of the most relevant scenarios of traffic systems. The asymmetric simple exclusion process (ASEP) with a defect is a minimal model for such a bottleneck scenario. One crucial question is "What is the critical strength of the defect that is required to create global effects, i.e. traffic jams localized at the defect position". Intuitively one would expect that already an arbitrarily small bottleneck strength leads to global effects in the system, e.g. a reduction of the maximal current. Therefore it came as a surprise when, based on computer simulations, it was claimed that the reaction of the system depends in non-continuous way on the defect strength and weak defects do not have a global influence on the system. Here we reconcile intuition and simulations by showing that indeed the critical defect strength is zero. We discuss the implications for the analysis of empirical and numerical data.
Box model for channels of human migration
Nikolay K. Vitanov, Kaloyan N. Vitanov
We discuss a mathematical model of migration channel based on the truncated Waring distribution. The truncated Waring distribution is obtained for a more general model of motion of substance through a channel containing finite number of boxes. The model is applied then for case of migrants moving through a channel consisting of finite number of countries or cities. The number of migrants in the channel strongly depends on the number of migrants that enter the channel through the country of entrance. It is shown that if the final destination country is very popular then large percentage of migrants may concentrate there.
Modeling the dynamics of dissent
Eun Lee, Petter Holme, Sang Hoon Lee
We investigate opinion formation against authority in an authoritarian society composed of agents with different levels of authority. We explore a (symbolically) "right" opinion, held by lower-ranking, obedient, less authoritative people, spreading in an environment of a "wrong" opinion held by authoritative leaders. The mental picture would be that of a corrupt society where the ruled people revolts against authority, but it could be argued to hold in more general situations. In our model, agents can change their opinion depending on the relative authority to their neighbors and their own confidence level. In addition, with a certain probability, agents can override the authority to take the right opinion of a neighbor. Based on analytic derivation and numerical simulations, we observe that both the network structure and heterogeneity in authority, and their correlation significantly affect the possibility of the right opinion to spread in the population. In particular, the right opinion is suppressed when the authority distribution is very heterogeneous and there is a positive correlation between the authority and number of neighbors of people. Except for such extreme cases, the spreading of the right opinion from the obedient agents takes place when there exist a tendency to override the authority to take the right opinion, but it can take a long time depending on the model parameters. We argue that the underlying social structure of agents sets the time scale of reaching consensus, based on the analysis of the underlying social relations.
Opinion dynamics over complex networks: kinetic modeling and numerical methods
Giacomo Albi, Lorenzo Pareschi, Mattia Zanella
In this paper we consider the modeling of opinion dynamics over time dependent large scale networks. A kinetic description of the agents' distribution over the evolving network is considered which combines an opinion update based on binary interactions between agents with a dynamic creation and removal process of new connections. The number of connections of each agent influences the spreading of opinions in the network but also the way connections are created is influenced by the agents' opinion. The evolution of the network of connections is studied by showing that its asymptotic behavior is consistent both with Poisson distributions and truncated power-laws. In order to study the large time behavior of the opinion dynamics a mean field description is derived which allows to compute exact stationary solutions in some simplified situations. Numerical methods which are capable to describe correctly the large time behavior of the system are also introduced and discussed. Finally, several numerical examples showing the influence of the agents' number of connections in the opinion dynamics are reported.
Collective intelligence: aggregation of information from neighbors in a guessing game
Toni Pérez, Jordi Zamora, Víctor M. Eguíluz
Complex systems show the capacity to aggregate information and to display coordinated activity. In the case of social systems the interaction of different individuals leads to the emergence of norms, trends in political positions, opinions, cultural traits, and even scientific progress. Examples of collective behavior can be observed in activities like the Wikipedia and Linux, where individuals aggregate their knowledge for the benefit of the community, and citizen science, where the potential of collectives to solve complex problems is exploited. Here, we conducted an online experiment to investigate the performance of a collective when solving a guessing problem in which each actor is endowed with partial information and placed as the nodes of an interaction network. We measure the performance of the collective in terms of the temporal evolution of the accuracy, finding no statistical difference in the performance for two classes of networks, regular lattices and random networks. We also determine that a Bayesian description captures the behavior pattern the individuals follow in aggregating information from neighbors to make decisions. In comparison with other simple decision models, the strategy followed by the players reveals a suboptimal performance of the collective. Our contribution provides the basis for the micro-macro connection between individual based descriptions and collective phenomena.
Dynamics on networks: competition of temporal and topological correlations
Oriol Artime, Jose J. Ramasco, Maxi San Miguel
Links in many real-world networks activate and deactivate in correspondence to the sporadic interactions between the elements of the system. The activation patterns may be irregular or bursty and play an important role on the dynamics of processes taking place in the network. Social networks and information or disease spreading processes are paradigmatic examples of this situation. Besides the burstiness, several other correlations may appear in the network dynamics. The activation of links connecting to the same node can be synchronized or the existence of communities in the network may mediate the activation patterns of internal an external links. Here we study the competition of topological and temporal correlations in link activation and how they affect the dynamics of systems running on the network. Interestingly, both types of correlations by separate have opposite effects: one (topological) delays the dynamics of processes on the network, while the other (temporal) accelerates it. When they occur together, our results show that the direction and intensity of the final outcome depends on the combination in a non trivial way.
Emergent dynamics of the Cucker-Smale flocking model and its variants
Young-Pil Choi, Seung-Yeal Ha, Zhuchun Li
In this chapter, we present the Cucker-Smale type flocking models, and discuss their mathematical structures and flocking theorems in terms of coupling strength, interaction topologies and initial data. In 2007, two mathematicians Felipe Cucker and Steve Smale introduced a second-order particle model which resembles Newton's equations in N-body system, and present how their simple model can exhibit emergent flocking behavior under sufficient conditions expressed only in terms of parameters and initial data. After Cucker-Smale's seminal works, their model has received lots of attention from applied math and control engineering communities. We discuss the state-of-art for the flocking theorems to Cucker-Smale type flocking models.
Leaders should not be conformists in evolutionary social dilemmas
Attila Szolnoki, Matjaz Perc
Szolnoki, Attila, and Matjaž Perc. "Leaders should not be conformists in evolutionary social dilemmas." Scientific Reports 6 (2016).
The most common assumption in evolutionary game theory is that players should adopt a strategy that warrants the highest payoff. However, recent studies indicate that the spatial selection for cooperation is enhanced if an appropriate fraction of the population chooses the most common rather than the most profitable strategy within the interaction range. Such conformity might be due to herding instincts or crowd behavior in humans and social animals. In a heterogeneous population where individuals differ in their degree, collective influence, or other traits, an unanswered question remains who should conform. Selecting conformists randomly is the simplest choice, but it is neither a realistic nor the optimal one. We show that, regardless of the source of heterogeneity and game parametrization, socially the most favorable outcomes emerge if the masses conform. On the other hand, forcing leaders to conform significantly hinders the constructive interplay between heterogeneity and coordination, leading to evolutionary outcomes that are worse still than if conformists were chosen randomly. We conclude that leaders must be able to create a following for network reciprocity to be optimally augmented by conformity. In the opposite case, when leaders are castrated and made to follow, the failure of coordination impairs the evolution of cooperation.
A review on attractive-repulsive hydrodynamics for consensus in collective behavior
José A. Carrillo, Young-Pil Choi, Sergio Pérez
This survey summarizes and illustrates the main qualitative properties of hydrodynamics models for collective behavior. These models include a velocity consensus term together with attractive-repulsive potentials leading to non-trivial flock profiles. The connection between the underlying particle systems to the swarming hydrodynamic equations is performed through kinetic theory modelling arguments. We focus on Lagrangian schemes for the hydrodynamic systems showing the different qualitative behavior of the systems and its capability of keeping properties of the original particle models. We illustrate known results concerning large time profiles and blow-up in finite time of the hydrodynamic systems to validate the numerical scheme. We finally explore unknown situations making use of the numerical scheme showcasing a number of conjectures based on the numerical results.
Dynamics of Transformation from Segregation to Mixed Wealth Cities
Anand Sahasranaman, Henrik Jeldtoft Jensen
We model the dynamics of the Schelling model for agents described simply by a continuously distributed variable - wealth. Agents move to neighborhoods where their wealth is not lesser than that of some proportion of their neighbors, the threshold level. As in the case of the classic Schelling model where segregation obtains between two races, we find here that wealth-based segregation occurs and persists. However, introducing uncertainty into the decision to move - that is, with some probability, if agents are allowed to move even though the threshold level condition is contravened - we find that even for small proportions of such disallowed moves, the dynamics no longer yield segregation but instead sharply transition into a persistent mixed wealth distribution. We investigate the nature of this sharp transformation between segregated and mixed states, and find that it is because of a non-linear relationship between allowed moves and disallowed moves. For small increases in disallowed moves, there is a rapid corresponding increase in allowed moves, but this tapers off as the fraction of disallowed moves increase further and finally settles at a stable value, remaining invariant to any further increase in disallowed moves. It is the overall effect of the dynamics in the initial region (with small numbers of disallowed moves) that shifts the system away from a state of segregation rapidly to a mixed wealth state. The contravention of the tolerance condition could be interpreted as public policy interventions like minimal levels of social housing or housing benefit transfers to poorer households. Our finding therefore suggests that it might require only very limited levels of such public intervention - just sufficient to enable a small fraction of disallowed moves, because the dynamics generated by such moves could spur the transformation from a segregated to mixed equilibrium.
The Aw-Rascle-Zhang model with constraints
Stefano Villa
The thesis deals with the Aw-Rascle-Zhang model for traffic. We have applied the model to describe the influence of a large and slow vehicle (a bus or a truck) on the traffic. The trajectory of the bus is given by an ODE. The model can also be applied to the case of a fixed constraint, like a traffic light or a toll gate. We define two different Riemann solvers: the first one conserves both the number of cars and the generalized momentum, while the second conserves only the number of cars. We characterize the invariant domains for these Riemann solvers. We study two numerical methods based on the Godunov method to capture the proposed solutions and we track the bus trajectory with a front-tracking technique. The first method is based on conservation and captures exactly the solution corresponding to the first Riemann solver. The second method is based on a non-uniform mesh. Both methods fail to capture the solutions corresponding to the second Riemann solver for general initial data. Finally, we prove the existence of solutions for the Cauchy problem for the second Riemann solver in the case of a fixed constraint, applying the wave-front tracking method.
Dynamics of epidemic spreading with vaccination: impact of social pressure and engagement
Marcelo A. Pires, Nuno Crokidakis
In this work we consider a model of epidemic spreading coupled with an opinion dynamics in a fully-connected population. Regarding the opinion dynamics, the individuals may be in two distinct states, namely in favor or against a vaccination campaign. Individuals against the vaccination follow a standard SIS model, whereas the pro-vaccine individuals can also be in a third compartment, namely Vaccinated. In addition, the opinions change according to the majority-rule dynamics in groups with three individuals. We also consider that the vaccine can give permanent or temporary immunization to the individuals. By means of analytical calculations and computer simulations, we show that the opinion dynamics can drastically affect the disease propagation, and that the engagement of the pro-vaccine individuals can be crucial for stopping the epidemic spreading.
Evolutionary games on the lattice: death and birth of the fittest
Eric Foxall, Nicolas Lanchier
This paper investigates the long-term behavior of an interacting particle system of interest in the hot topic of evolutionary game theory. Each site of the d-dimensional integer lattice is occupied by a player who is characterized by one of two possible strategies. Following the traditional modeling approach of spatial games, the configuration is turned into a payoff landscape that assigns a payoff to each player based on her strategy and the strategy of her neighbors. The payoff is then interpreted as a fitness assuming that players independently update their strategy at rate one by mimicking their neighbor with the largest payoff. The mean-field approximation of this spatial game exhibits the same long-term behavior as the popular replicator equation. Except for a coexistence result that shows an agreement between the process and the mean-field model, our analysis reveals that the two models strongly disagree in a many aspects, showing in particular that the presence of a spatial structure in the form of local interactions plays a key role. More precisely, in the parameter region where both strategies are evolutionary stable in the replicator equation, either one strategy wins or the system fixates in a configuration where both strategies are present for the spatial game. In addition, while defection is always evolutionary stable for the prisoner's dilemma game in the replicator equation, space favors cooperation in our model.
Matthew O. Jackson
The "friendship paradox" (Feld 1991) is the structural implication of networks that, on average, peoples' friends have strictly more friends than the average person in a network. In particular, the number of people who observe a given person is proportional to the number of connections that the person has. This can distort perceptions of norms and behavior if more popular people in a society behave differently from less popular people. As I show here there are two things that drive people with more friends to behave differently from people with fewer friends. The first is that in any setting with strategic complementarities, people with more friends are exposed to greater interaction and influence. The second is that people who benefit more from a given activity will tend to form more relationships as they benefit more from the complementarities. These two effects lead people with more friends to choose more extreme actions, which in turn feeds back via the the friendship paradox to increase overall perceptions of behavior and then via complementarities to amplify average behavior. These theoretical results are consistent with the multitude of studies finding that students (from middle school through university) consistently overestimate peer consumption of alcohol, cigarettes, and drugs. This in turn amplifies students' own behaviors, and can help explain problems with adolescent abuse of drugs and alcohol, as well as other behaviors. I also discuss how these results change in cases of strategic substitutes, where individuals overestimate free-riding by peers.
Modelling a network where the opinion of each unit varies according to a majority ruling of its neighbouring units
V. F. Kusmartsev, F. V. Kusmartsev
The complexity of human behaviour can lead to very unpredictable patterns in social activity and structure. Here we demonstrate the instability of a community network controlled by majority ruling, where an element adopts the most popular opinion of their peers. We modelled a community as a square lattice, and performed sequential time step numerical calculations upon each cell in parallel. Depending on the initial ratio of two opinions, the community can segregate either into separate gangs and cliques, or get dominated by a single opinion. We also note that gangs are separated by neutral or confused groups of individuals, buffering the transition. The behaviors shown by this model can be comfortably applied to many other real life situations, such as neural or ecological networks. The results of this paper have been preliminary published in the Ref. [34].
C.-Y. Xia, S. Meloni, M. Perc, Y. Moreno, to appear in Europhysics Letters (2015)
Dynamic instability of cooperation due to diverse activity patterns in evolutionary social dilemmas
Individuals might abstain from participating in an instance of an evolutionary game for various reasons, ranging from lack of interest to risk aversion. In order to understand the consequences of such diverse activity patterns on the evolution of cooperation, we study a weak prisoner's dilemma where each player's participation is probabilistic rather than certain. Players that do not participate get a null payoff and are unable to replicate. We show that inactivity introduces cascading failures of cooperation, which are particularly severe on scale-free networks with frequently inactive hubs. The drops in the fraction of cooperators are sudden, while the spatiotemporal reorganization of compact cooperative clusters, and thus the recovery, takes time. Nevertheless, if the activity of players is directly proportional to their degree, or if the interaction network is not strongly heterogeneous, the overall evolution of cooperation is not impaired. This is because inactivity negatively affects the potency of low-degree defectors, who are hence unable to utilize on their inherent evolutionary advantage. Between cascading failures, the fraction of cooperators is therefore higher than usual, which lastly balances out the asymmetric dynamic instabilities that emerge due to intermittent blackouts of cooperative hubs.