Singularidades aisladas

SINGULARIDADES AISLADAS

Series de Laurent

Si f(z) es holomorfa en un disco D = {z ∈ ℂ: |z - z₀| < R}, la serie de Taylor permite representar a f(z) en serie potencias no negativas de z - z₀ para todo z ∈ D:

∞∑ n f(n)(z0) f (z) = an(z - z0), con an = n! y z ∈ D. n=0

Esto no aplica por ejemplo para 1∕z o e^z∕z² alrededor de 0. Para este tipo de funciones se utiliza la serie de Laurent, que involucra potencias positivas y negativas de z - z₀.

Teorema (Expansión de Laurent). Sea f holomorfa en la región anular D = {z ∈ ℂ: r₁ < |z - z₀| < r₂} y sea C cualquier contorno cerrado simple alrededor de z₀ orientado positivamente y contenido en D. Entonces, para todo z ∈ D

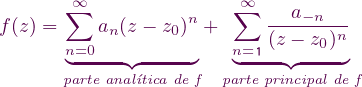
∑∞ n ∑∞ --a-n--- f(z) = an(z - z0) + (z - z0)n n◟=0---◝◜----◞ n◟=0--◝◜----◞ parte analˊitica de f parte principal de f

donde

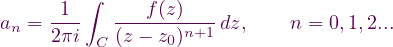
∫ a = -1- ---f(z)---dz, n = 0,1,2... n 2πi C(z - z0)n+1

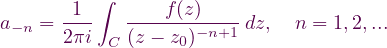
1 ∫ f(z) a-n = 2πi C (z --z0)--n+1-dz, n = 1,2,...

Singularidades aisladas

Un punto z₀ es una singularidad aislada de f si f no es holomorfa en z₀ pero sí lo es un un entorno reducido de z₀, esto es, 0 < |z -z₀|≤ R para algún R > 0, es decir, un disco de radio R centrado en z₀ pero in incluir el centro.

Si z₀ es un punto singular aislado de f, entonces f es holomorfa en cualquier disco reducido 0 < |z - z₀|≤ R, y admite la representación

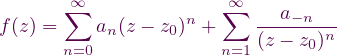
∞ ∞ ∑ n ∑ --a-n--- f(z) = n=0an(z - z0) + n=1 (z - z0)n

para 0 < |z - z₀| < R.

Clasificación. Si el desarrollo de serie de Laurent en un entorno reducido de punto singular aislado z₀ no tiene términos con potencias negativas, entonces z₀ es una singularidad evitable; si tiene un número finito no nulo de términos con potencias negativas, es un polo. Si tiene infinitos términos no nulos con potencias negativas, es una singularidad esencial. Es decir,

si a_-n = 0 para todo n ∈ ℕ, z₀ es una singularidad evitable,
si a_-m≠0 y a_-n = 0 para todo n > m, z₀ es un polo de orden m,
si hay infinitos a_-n≠0, z₀ es una singularidad esencial.

Singularidades evitables

Si f tiene una singularidad evitable en z₀ entonces

∞∑ f(z) = an(z - z0)n. n=0

De esto sigue que la serie puede ser evaluada en cualquier z perteneciente al disco |z - z₀| < R, y f será holomorfa en ese disco. Además

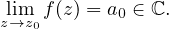
lim f(z) = a0 ∈ ℂ. z→z0

En resumen tenemos que:

Teorema. Son equivalentes

z₀ es una singularidad evitable de f
lim_z→z₀f(z) = w₀ ∈ ℂ existe.
lim_z→z₀(z - z₀)f(z) = 0.
|f| está acotada en un entorno de z₀.

Ejemplo: singularidad evitable en el origen

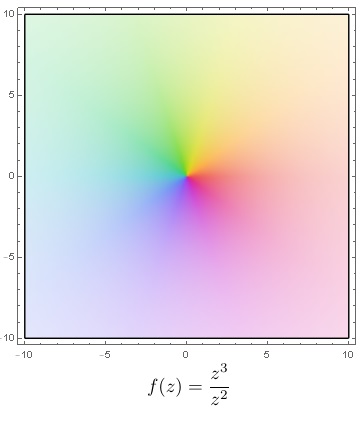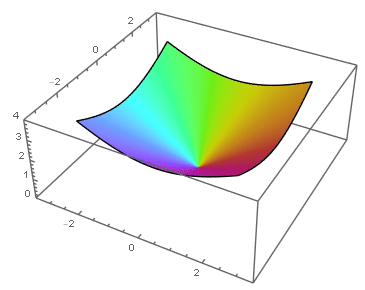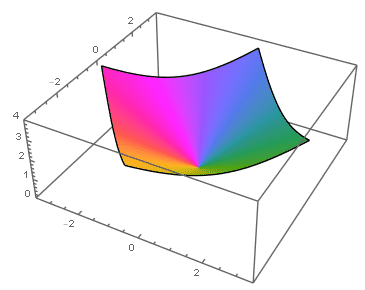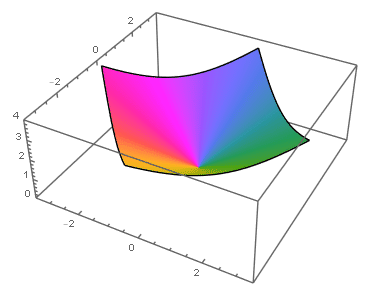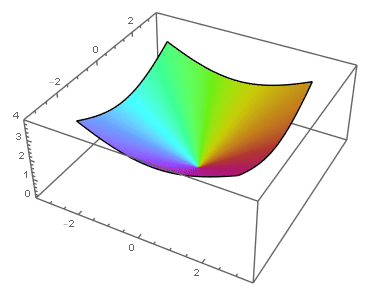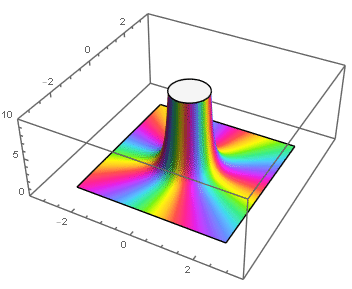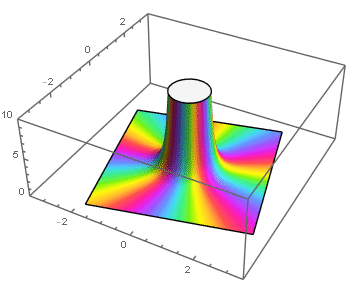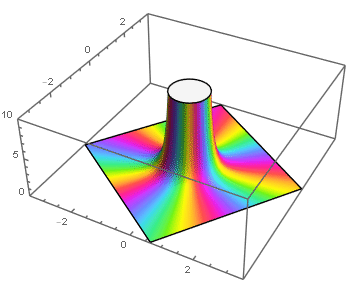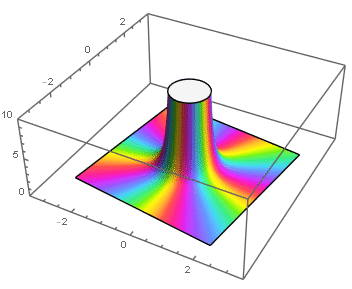
Polos

Si f tiene un polo de orden m en z₀, entonces para z en el disco 0 < |z -z₀| < R, f tiene desarrollo

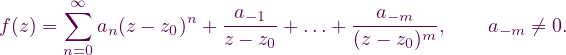
∑∞ n -a--1- --a-m--- f(z) = an(z - z0) + z - z0 + ...+ (z - z0)m , a-m ⁄= 0. n=0

Como

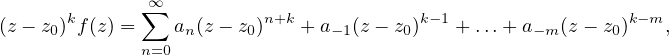
k ∞∑ n+k k-1 k-m (z - z0)f (z) = an(z - z0) + a-1(z - z0) +...+ a-m (z - z0) , n=0

obtenemos que

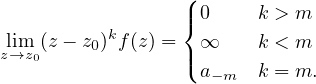
( |{ 0 k > m lim (z - z)kf(z) = ∞ k < m z→z0 0 |( a-m k = m.

Es decir, que f tenga un polo de orden m en z₀ equivale a que (z -z₀)^kf(z) tienda a número complejo no nulo cuando z → z₀, que de hecho será el coeficiente a_-m del desarrollo en serie de Laurent centrado en el disco reducido 0 < |z - z₀| < R.

En particular,

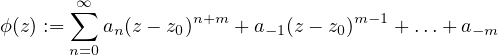
∑∞ n+m m- 1 ϕ(z) := an(z - z0) +a- 1(z - z0) + ...+ a- m n=0

está bien definida en z₀, por lo que es holomorfa en |z -z₀| < R, y ϕ(z₀) = a_-m≠0, lo que permite escribir a f como

--ϕ(z)-- f(z) = (z - z0)m .

En resumen tenemos:

Teorema. Tenemos las siguientes caracterizaciones de polos de f.

z₀ es un polo de f ⇐⇒ lim_z→z₀|f(z)| = ∞.
z₀ es un polo de orden m de f ⇐⇒ lim_z→z₀(z - z₀)^mf(z) ∈ ℂ_≠0.

Ejemplos: polo de orden 1 y 5 en el origen:

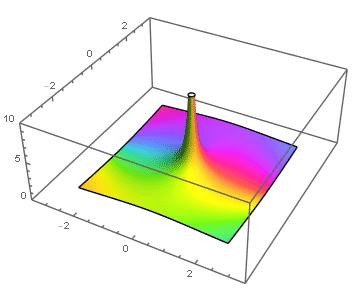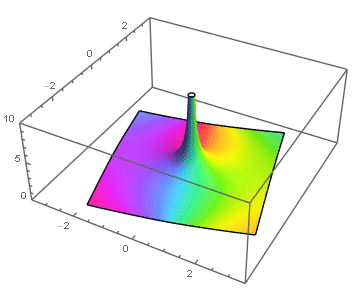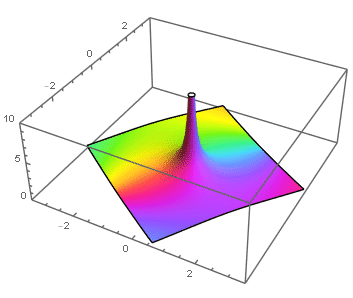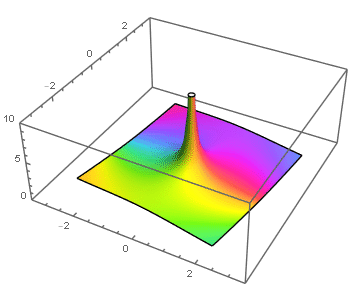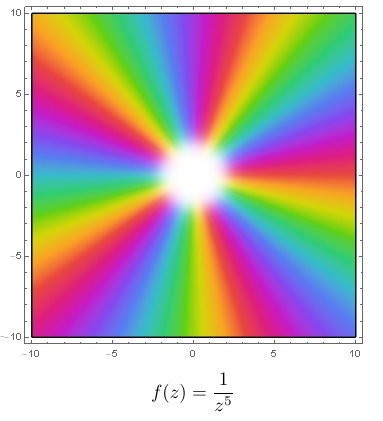Singularidades esenciales

Si f tiene una singularidad esencial en z₀, entonces para z en el disco 0 < |z -z₀| < R, f tiene desarrollo

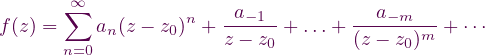
∑∞ n -a-1-- --a-m--- f(z) = an(z - z0) + z - z0 + ...+ (z - z0)m + ⋅⋅⋅ n=0

para una cantidad infinita de potencias negativas.

Teorema. Son equivalentes

z₀ es una singularidad esencial de f.
El límite lim_z→z₀f(z) no existe.

El siguiente teorema nos dice que f está arbitrariamente cerca de cualquier complejo contenido en un entorno de z₀.

Teorema (Teorema de Casorati-Weierstrass). Si f tiene una singularidad aislada esencial en z₀, y w ∈ ℂ, entonces existe una sucesión {z_n}_n ∈ ℂ tal que z_n → z₀ y f(z_n) → w.

El resultado anterior es ampliado por el siguiente teorema, que establece que f asume cada valor complejo salvo una posible excepsión.

Teorema (Teorema grande de Picard). Sea z₀ una singularidad aislada esencial de f y sea D un disco reducido 0 < |z - z₀| < R donde f es holomorfa. Entonces f(D) es todo el plano complejo ℂ excepto a lo sumo un punto.

Ejemplos: singularidades esenciales en el origen:
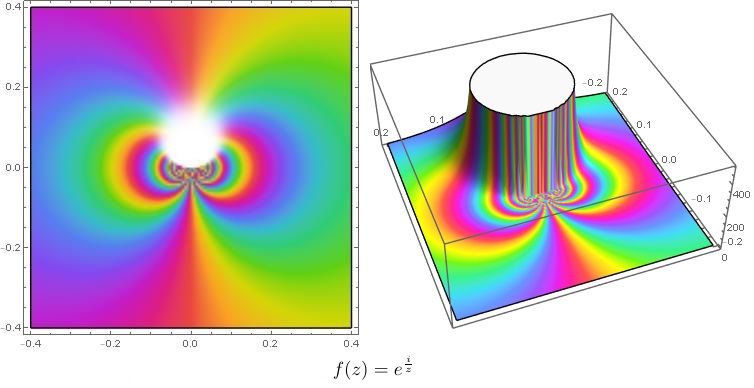
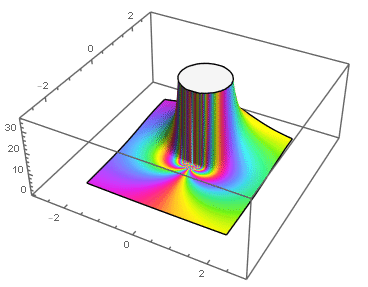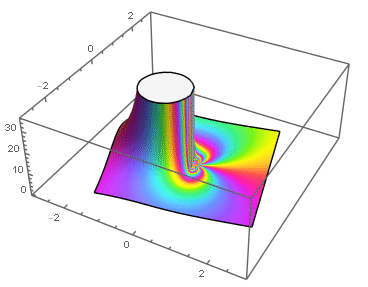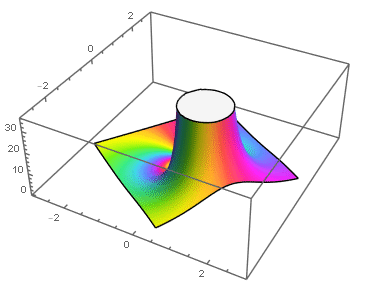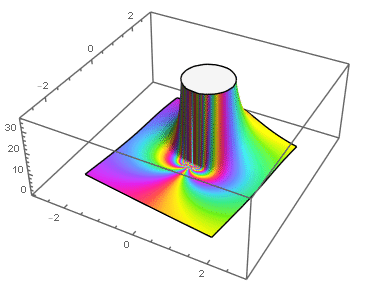
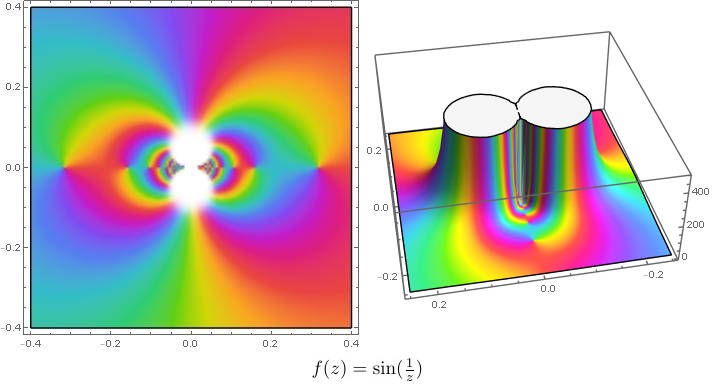
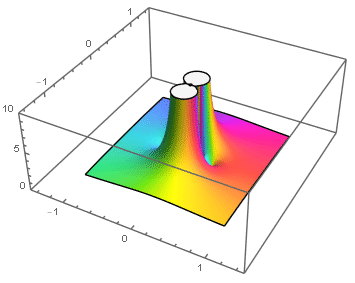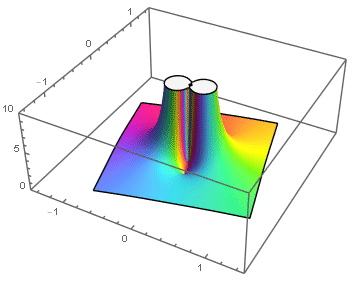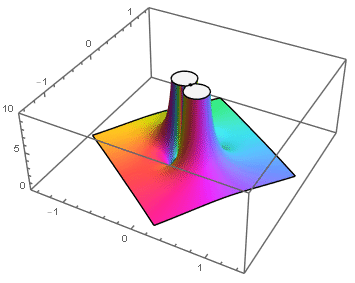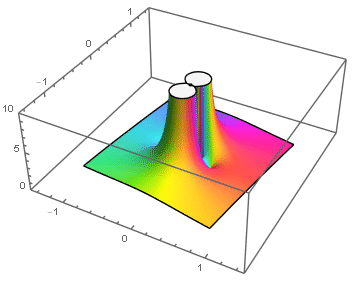