Many people post their objects of study in their web pages. I decided to do the same thing, so here is my own zoo. It's kind of esoteric, but certainly nice: finite dimensional Nichols algebras over braided vector spaces of nonabelian group type.

Any braided vector space gives rise to a Nichols algebra, as first found by Nichols in
[W. Nichols, Bialgebras of type one, Comm. Algebra 6 15 (1978), 1521-1552].
See [AG1, math.QA/9802074] for definitions.
See [G1 weyl.ps.gz] for a definition of derivations and how to use them. Also for the definition of "group type".
See [G2 nald.ps.gz] for some examples.
See [AG2, math.QA/0202084] for more examples.
These are certainly not the only references, but they are written in the way I like (of course!).
Other references are
[MS]
[AS1, math.QA/9803058]
[AS2, math.QA/0110136]

Lest you think you never saw a Nichols algebra, let me mention two examples: symmetric and antisymmetric ( = exterior) algebras are Nichols. But there are a lot of examples you might have seen; here is a list of papers in which they appeared under various names:
[G. Lusztig, Introduction to Quantum Groups, Birkhäuser, 1993.]
[M. Rosso, Certaines formes bilineaires sur les groupes quantiques et une conjecture de Schechtman et Varchenko, CRAS Paris, 314, Sèrie I (1992), 5-8.]
[M. Rosso, Groupes quantiques et algèbres de battage quantiques, CRAS Paris, 320, Sèrie I (1995), 145-148.]
[P. Schauenburg, A Characterization of the Borel-like Subalgebras of Quantum Enveloping Algebras, Comm. in Algebra 24 (1996), 9, 2811-2823]
[S.L. Woronowicz, Differential Calculus on Compact Matrix Pseudogroups (Quantum Groups), Comm. Math. Phys. 122 (1989), 125-170]

So here are all examples I know about of finite dimensional Nichols algebras of nonabelian group type (here by "nonabelian group type" we mean that the braided vector space does not live in a category of modules over the Drinfeld double of an abelian group). All of them are presented by means of quandles and cocycles, as explained in [AG2].

dim V = 3

The quandle is X = {0, 1, 2}, affine, with g = -1. This means i » j = 2i - j (mod 3). The cocycle is q = -1. This means c (i,j) = -(2i-j, i). The Nichols algebra has dimension 12. It is generated by x0, x1, x2, and has relations

x02 = x12 = x22 = 0,
x0x1+x1x2+x2x0 = 0,
x1x0+x2x1+x0x2 = 0.

Besides these relations, to have a Gröbner basis we have to add the relation

x0x1x0=x1x0x1.

A basis is given then by multiplying one element in each row from top to bottom in all the possible ways:

The Hilbert polynomial is

(1+t)2(1+t+t2) = 1+3t+4t2+3t3+t4

Little history:
This algebra was first discovered by Milinski and Schneider around 1996. The original preprint was published 4 years later [MS].

dim V = 4

The quandle is X = {0, 1, 2, 3}, representing the vertices of a tetrahedron. The action i » j fixes i and rotates the other three elements by a third of a turn with the left hand rule (or the right hand, but with the left is more progressive).
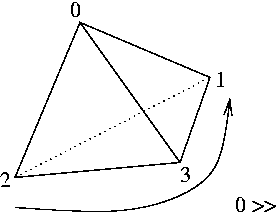
action in the tetrahedron

The cocycle is q = -1. The algebra has dimension 72. It is generated by x0, x1, x2, x3, and has relations

x02 = x12 = x22 = x32 = 0,
x3x2+x2x1+x1x3 = 0,
x3x1+x1x0+x0x3 = 0,
x3x0+x0x2+x2x3 = 0,
x2x0+x0x1+x1x2 = 0,
x2x1x0x2x1x0 +x1x0x2x1x0x2 +x0x2x1x0x2x1 = 0.

A basis is given then by multiplying one element in each row from top to bottom in all the possible ways:

The Hilbert polynomial is then

(1+t)2(1+t+t2)2(1+t3) = t9 + 4 t8 + 8 t7 + 11 t6 + 12 t5 + 12 t4 + 11 t3 + 8 t2 + 4 t + 1.

Little history:
This algebra appeared first in [G2]. It arose as a computable Nichols algebra on a braided vector spaces of group type of dimension 4.

dim V = 5

The quandle is X = {0, 1, 2, 3, 4} = Z/5Z, affine, with g = 2. One can take also g = 3, both algebras are dual to each other. This is, i » j = -i + 2j (mod 5). The cocycle is constant q = -1, i.e., c(i,j) = -(-i+2j,i). The algebra has dimension 1280. It is generated by x0, x1, x2, x3, x4, and has relations

x02 = x12 = x22 = x32 = x42 = 0,
x3x2+x2x0 +x1x3+x0x1 = 0,
x4x0+x2x1 +x1x4+x0x2 = 0,
x4x1+x3x4 +x1x0+x0x3 = 0,
x4x2+x3x0 +x2x3+x0x4 = 0,
x4x3+x3x1 +x2x4+x1x2 = 0,
x1x0x1x0 +x0x1x0x1 = 0.

A basis is given then by multiplying one element in each row from top to bottom in all the possible ways:

The Hilbert polynomial is then

(1 + t)2 (1 + t + t2 + t3 ) (1 + t + 2 t2 + 2 t3 + 2 t4 + t5 + t6) (1+t+2t2+2t3+t4+t5)
= t16 + 5 t15 + 15 t14 + 35 t13 + 66 t12 + 105 t11 + 145 t10 + 175 t9 + 186 t8 + 175 t7 + 145 t6 + 105 t5 + 66 t4 + 35 t3 + 15 t2 + 5 t + 1.

Little history:
This appeared in [AG2]. The relation in degree 4 was generalized there to affine quandles such that -g has order 4.

dim V = 6

There are two related examples here. Take first X = {1,2,3,4,5,6} the faces of a cube (as in a dice, 1 opposed to 6, 2 to 5 and 3 to 4). The action is similar to that of the tetrahedron: i » j fixes i and rotates the cube 1/4 of a turn. The cocycle is q = -1. The algebra has dimension 576. It is generated by x1, x2, x3, x4, x5, x6, and has relations

x12 = x22 = x32 = x42 = x52 = x62 = 0,
x4x3+x3x4 = 0
x5x2+x2x5 = 0
x6x1+x1x6 = 0
x3x2+x2x1+x1x3 = 0
x4x1+x2x4+x1x2 = 0
x5x1+x4x5+x1x4 = 0
x5x3+x3x1+x1x5 = 0
x6x2+x2x3+x3x6 = 0
x6x3+x5x6+x3x5 = 0
x6x4+x4x2+x2x6 = 0
x6x5+x5x4+x4x6 = 0

A Gröbner basis is given in this file; the variables x1,...,x6 here are called a,...,f there.

A basis is given then by multiplying one element in each row from top to bottom in all the possible ways:

The Hilbert polynomial is then

(1 + t)2 (1 + t + t2 )2 (1 + t + t2 + t3 )2
= t12 + 6t11 + 19t10 + 42t9 + 71t8 + 96t7 + 106t6 + 96t5 + 71t4 + 42t3 + 19t2 + 6t + 1.

A similar example is given by the transpositions in S4 with the cocycle q = -1. The algebra then has generators x0, x1, x2, x3, x4, x5 (with some identification) and has relations

x02 = x12 = x22 = x32 = x42 = x52 = 0,
x3x2+x2x3 = 0
x4x1+x1x4 = 0
x5x0+x0x5 = 0
x3x0+x1x3+x0x1 = 0
x3x1+x0x3+x1x0 = 0
x4x0+x2x4+x0x2 = 0
x4x2+x0x4+x2x0 = 0
x5x1+x2x5+x1x2 = 0
x5x2+x1x5+x2x1 = 0
x5x3+x4x5+x3x4 = 0
x5x4+x3x5+x4x3 = 0

A Gröbner basis is given in this file; the variables x0,...,x5 here are called a,...,f there.

The dimension and the Hilbert polynomial are the same. Notice that both algebras are different in principle, the relations are not exactly the same though they look similar. Indeed, they are different as braided Hopf algebras.

Little history:
The example in S4 appeared in [MS]. The example with the cube appeared in [AG2], together with the relationship between them.

dim V = 7

Take X = Z/7Z, affine, g = 3 or g = 5 (they will yield dual algebras). We use g = 3 in what follows, we have i » j = 5i+3j (mod 7). Again q = -1. The algebra then has dimension 326592, with generators x0, x1, x2, x3, x4, x5, x6 and relations

x02 = x12 = x22 = x32 = x42 = x52 = x62 = 0
x3x0 + x1x3 + x0x1 = 0
x3x2 + x2x0 + x0x3 = 0
x4x1 + x2x4 + x1x2 = 0
x4x3 + x3x1 + x1x4 = 0
x5x0 + x4x5 + x0x4 = 0
x5x1 + x1x0 + x0x5 = 0
x5x2 + x3x5 + x2x3 = 0
x5x4 + x4x2 + x2x5 = 0
x6x0 + x2x6 + x0x2 = 0
x6x1 + x5x6 + x1x5 = 0
x6x2 + x2x1 + x1x6 = 0
x6x3 + x4x6 + x3x4 = 0
x6x4 + x4x0 + x0x6 = 0
x6x5 + x5x3 + x3x6 = 0
x2x0x1x2x0x1 + x1x2x0x1x2x0 + x0x1x2x0x1x2 = 0

A Gröbner basis is given in this file; the variables x0,...,x6 here are called a,...,g there.

A basis is given then by multiplying one element in each row from top to bottom in all the possible ways:

Hilbert polynomial:

(1 + t)2 (1 + t + t2)2 (1 + t + 2t2 + 3t3 + 4t4 + 5t5 + 4t6 + 5t7 + 4t8 + 3t9 + 2t10 + t11 + t12) (1 + t + t2 + 2t3 + 2t4 + 2t5 + 2t6 + t7 + t8 + t9) (1 + t + 2t2 + 2t3 + 3t4 + 3t5 + 2t6 + 2t7 + t8 + t9)
=1t36 + 7t35 + 28t34 + 84t33 + 210t32 + 462t31 + 918t30 + 1673t29 + 2828t28 + 4473t27 + 6664t26 + 9394t25 + 12573t24 + 16023t23 + 19488t22 + 22659t21 + 25214t20 + 26873t19 + 27448t18 + 26873t17 + 25214t16 + 22659t15 + 19488t14 + 16023t13 + 12573t12 + 9394t11 + 6664t10 + 4473t9 + 2828t8 + 1673t7 + 918t6 + 462t5 + 210t4 + 84t3 + 28t2 + 7t + 1

Little history:
This example seemed to be the natural next step in [AG2]. However, it is computationally too consuming. The Gröbner basis has been computed by Jan-Erik Roos using the program Bergman on an alpha machine and it took about 1GB of memory in char 31 to reach degree 13 and in char 0 to reach degree 12. If one translates 30's by -1 and 29 by -2 in the basis for char 31, one gets in degree 13 two relations which can be proved to be relations in char 0 with my program deriva. With the program basis (or just by hand) one can find the basis, and again with deriva one can prove that the highest monomial doesn't vanish in the Nichols algebra. The conclusion is: we have it!

dim V = 10

Take X the conjugacy classes of transpositions in S5. As always, q = -1. The algebra then has dimension 8294400, with generators x0, x1, x2, x3, x4, x5, x6 x7, x8, x9, and relations

x02 = x12 = x22 = x32 = x42 = x52 = x62 = x72 = x82 = x92 = 0
x4x2+x2x4 = 0
x4x3+x3x4 = 0
x5x1+x1x5 = 0
x5x3+x3x5 = 0
x6x1+x1x6 = 0
x6x2+x2x6 = 0
x7x0+x0x7 = 0
x7x3+x3x7 = 0
x7x6+x6x7 = 0
x8x0+x0x8 = 0
x8x2+x2x8 = 0
x8x5+x5x8 = 0
x9x0+x0x9 = 0
x9x1+x1x9 = 0
x9x4+x4x9 = 0
x4x0+x1x4+x0x1 = 0
x4x1+x1x0+x0x4 = 0
x5x0+x2x5+x0x2 = 0
x5x2+x2x0+x0x5 = 0
x6x0+x3x6+x0x3 = 0
x6x3+x3x0+x0x6 = 0
x7x1+x2x7+x1x2 = 0
x7x2+x2x1+x1x7 = 0
x7x4+x5x7+x4x5 = 0
x7x5+x5x4+x4x7 = 0
x8x1+x3x8+x1x3 = 0
x8x3+x3x1+x1x8 = 0
x8x4+x6x8+x4x6 = 0
x8x6+x6x4+x4x8 = 0
x9x2+x3x9+x2x3 = 0
x9x3+x3x2+x2x9 = 0
x9x5+x6x9+x5x6 = 0
x9x6+x6x5+x5x9 = 0
x9x7+x8x9+x7x8 = 0
x9x8+x8x7+x7x9 = 0

A Gröbner basis is given in this file; the variables x0,...,x9 here are called a,...,j there.

A basis is given then by multiplying one element in each row from top to bottom in all the possible ways from this file.

Hilbert polynomial:

(1 + t)4 (1 + t + t2)3 (1 + t + 2t2 + 2t3 + t4 + t5)(1 + t + 3t2 + 6t3 + 9t4 + 13t5 + 19t6 + 24t7 + 27t8 + 31t9 + 32t10 + 31t11 + 27t12 + 24t13 + 19t14 + 13t15 + 9t16 + 6t17 + 3t18 + t19 + t20)(1 + t + 2t2 + 2t3 + t4 + t5)
= t40 + 10t39 + 55t38 + 220t37 + 711t36 + 1960t35 + 4761t34 + 10410t33 + 20796t32 + 38370t31 + 65921t30 + 106120t29 + 160857t28 + 230480t27 + 313121t26 + 404330t25 + 497207t24 + 583120t23 + 652942t22 + 698580t21 + 714456t20 + 698580t19 + 652942t18 + 583120t17 + 497207t16 + 404330t15 + 313121t14 + 230480t13 + 160857t12 + 106120t11 + 65921t10 + 38370t9 + 20796t8 + 10410t7 + 4761t6 + 1960t5 + 711t4 + 220t3 + 55t2 + 10t + 1

Little history:
Although the space V was first considered by Milinski-Schneider (as an obvious generalization for that in S3 and S4), they couldn't compute its dimension or even say if it was finite dimensional in the first version of their paper. Then the algebra appeared in [FK], the dimension was computed by Jan-Erik Roos with Bergman. They actually considered the algebra T(V)/K2, where K2 stands here for the relations in degree 2. The Gröbner basis was provided to me by J-E Roos. With it, as in the case of X = Z/7Z above, one can compute a highest degree element and with deriva prove that this element is nonzero in the Nichols algebra.

Bibliography


[AG1] N. Andruskiewitsch and M. Graña, Braided Hopf algebras over non-abelian groups, Bol. Acad. Ciencias (Córdoba) 63 (1999), 45-78. Also in math.QA/9802074.
[AG2] N. Andruskiewitsch and M. Graña, From racks to pointed Hopf algebras, Adv. Math. to appear. Also in math.QA/0202084.
[AS1] N. Andruskiewitsch and H-J. Schneider, Lifting of quantum linear spaces and pointed Hopf algebras of order p3, J. Algebra 209 (1998), 659-691. Also in math.QA/9803058.
[AS2] N. Andruskiewitsch and H-J. Schneider, Pointed Hopf Algebras, in "Recent developments in Hopf algebra theory", 1-68, MSRI Publications 43, Cambridge Univ. Press, Cambridge, 2002. Also in math.QA/0110136.
[G1] M. Graña, A freeness theorem for Nichols algebras, J. Algebra 231 1 (2000), 235-257. Also here.
[G2] M. Graña, On Nichols algebras of low dimension, in "New Trends in Hopf Algebra Theory"; Contemp. Math. 267 (2000), 111-136. Also here.
[FM] S. Fomin and A. N. Kirilov, Quadratic algebras, Dunkl elements, and Schubert calculus, Progr. Math. 172, Birkhauser, (1999), 146-182.
[MS] A. Milinski and H.-J. Schneider, Pointed Indecomposable Hopf Algebras over Coxeter Groups, in "New Trends in Hopf Algebra Theory"; Contemp. Math. 267 (2000), 215-236.