de diferentes filas y columnas

Suma Constante de elementos de diferentes filas y columnas

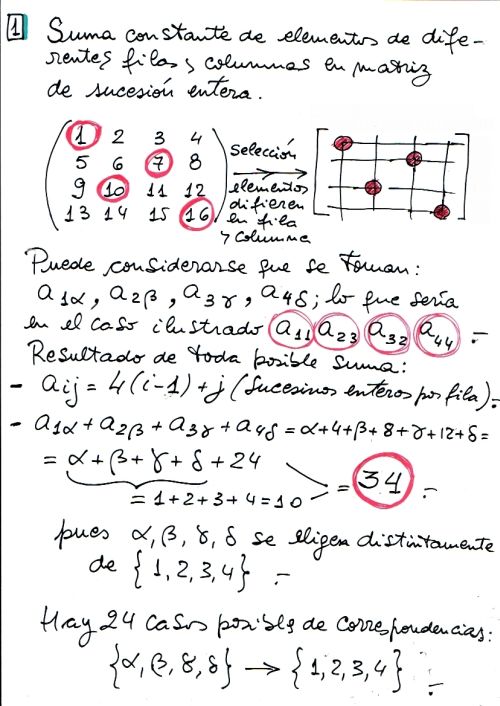
Hay una matriz de números enteros sucesivos coloreables con dos colores, rojo y amarillo, que pueden elegirse para cada número ubicado en alguna fila horizontal o columna vertical. Es interesante notar que coloreando distintamente a cuatro números, que tengan todos entre sí diferentes filas y columnas como se muestra en este ejemplo, cualesquiera sea la forma de elegirlos la suma de ellos da 34. Podemos pensar el problema partiendo de una matriz que tenga elegidos a los números de su diagonal como la ilustrada, y que claramente suman 34.

PARA PENSAR EL PROBLEMA

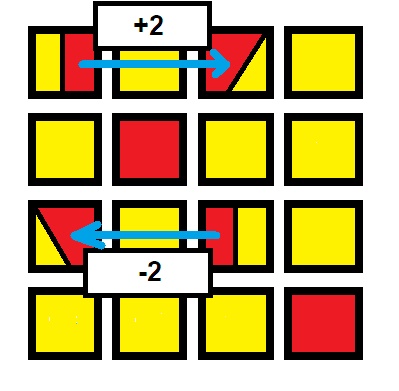
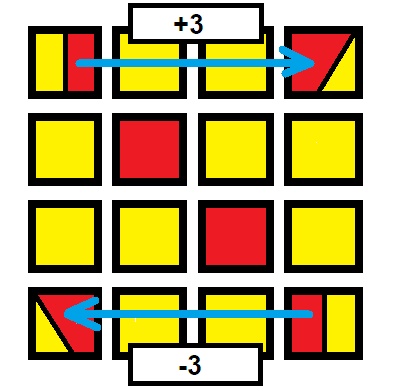
1- Definimos una operación de "intercambio" de columnas cuando se asignan todos los colores de una columna dada a otra y viceversa.

2- La operación de "intercambio" sigue manteniendo la propiedad de un solo número por fila y columna, ¿por qué?

3- La operación de "intercambio" sigue manteniendo la propiedad de que la suma de elegidos sea 34, ¿por qué?

4- Toda elección de cuatro números con uno solo por cada fila y columna puede también obtenerse, partiendo de una matriz con elegidos en su diagonal y luego realizando los "intercambios" necesarios entre las columnas. ¿por qué?

Ilustraciones para pensar.....

Desarrollos más teóricos