|
Un problema para entender
mediante la Teoría de Grafos.
---------------------------------------------------------------------------------
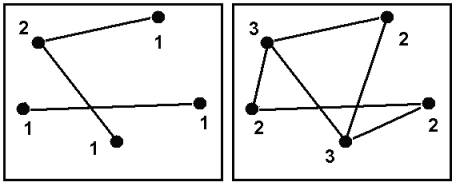
Un ingeniero de caminos debe revisar todas
las rutas que están entre las ciudades mostradas.
Puede entrar al complejo caminero por
alguna de las tres ciudades marcadas y salir del mismo por cualquiera de
todas las ciudades.
Por razones de economía conviene
que pase sólo una vez por cada una de todas las rutas entre las
ciudades.
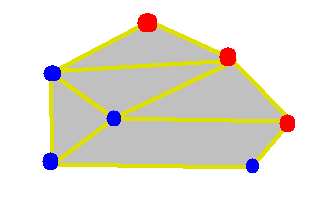
¿Por cuál ciudad deberá
entrar para lograrlo?
¿En cuál ciudad terminará
su trayecto y saldrá?
¿Por cuáles ciudades fue
pasando en este caso?
-----------------------------------------------------------------------------
Grafos Simples.-
Aquí lidiaremos con grafos simples,
es decir en los que hay una arista o lado entre vértices como máximo,
y en los que no hay loops o lazos que conectan algùn vértice
consigo mismo.
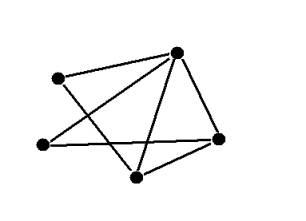
El problema del ingeniero permite ser
analizado mediante un grafo simple.
El grado de un nodo de un grafo simple
es la cantidad de aristas o lados que concurren a èl.
------------------------------------------------------------
Trayectorias y Circuitos.-
Si en un grafo simple se van recorriendo
sucesivamente sus aristas de modo tal que dos sucesivas sean adyacentes,
es decir que concurran al mismo vèrtice por el que se pasa de una
a la otra, se está recorriendo o determinando una trayectoria o
camino.
Cuando cierta trayectoria comienza y termina
en el mismo nodo decimos que es un circuito.
Cuando una trayectoria pasa sólo
una vez por todas y cada una de las aristas o lados se dice que la trayectoria
es semi- euleriana, y si esta trayectoria fuera un circuito se la denomina
circuito euleriano.
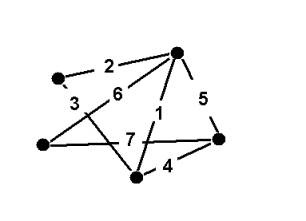
En el problema del ingeniero de caminos
necesitamos saber si hay trayectorias semi-eulerianas y por qué
vértices pueden comenzar y terminar.
-----------------------------------------------------------
Tratamiento del lema del apretón
de manos.-
No existe un grafo simple con un sólo
nodo de grado impar.
Esto refiere entre otros temasa las paridades
de los nodos de un grafo simple, es decir cuántos nodos pares e
impares tiene.
Dado cierto grafo, al agregarle una arista,
a cada nodo de los extremos de esta arista se le suma una unidad a su grado.
Es decir, que si alguno de esos nodos
de los extremos tenían grado impar, pasan a tener grado par y viceversa.
Analizando las posibles combinaciones
de paridades de estos nodos de los extremos del nuevo vértice:
i) par-par,
ii) par-impar,
iii)impar-impar,
se nota que la cantidad de nodos con grados
impares resulta:
i)o aumentada en dos unidades,
ii)o inalterada,
iii)o reducida en dos unidades.
Para mostrar esto se toma un cierto conjunto
de puntos del plano sin vértices que los conecten, y se lo considera
un grafo sin vértices. Claramente todo nodo en este caso tiene grado
cero.
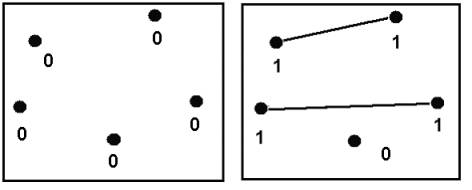
Cualquier grafo simple puede entonces obtenerse
partiendo de unir los nodos de un grafo sin aristas, agregando
sucesivamente sus aristas, hasta completarlo.
A partir de esto puede afirmarse que todo
grafo simple tiene o ningún nodo de grado impar o por lo menos dos
nodos de grado impar.
Es decir, no existe un grafo simple con
un sólo nodo de grado impar.
----------------------------------------------------------------------
Paridad de nodos y trayectorias semi-eulerianas.-
La teoría de grafos nos garantiza
la existencia de una trayectoria semi- euleriana cuando sólo dos
nodos tengan grado impar.
Queda claro que si hubiese más
nodos impares ya tendrían que ser comienzos o fines y no existen
trayectorias que pasen por todas las aristas con varios comienzos y fines.
Notemos que en el problema del ingeniero
serán estos nodos impares los de inicio y final de la trayectoria
que pasará por todos las aristas.
-------------------------------------------------------------- |




