Dado un conjunto de puntos en el espacio, puede tomárselos para ilustrar lo que en matemática se denomina un grafo.
 Para ello si lo representado por un punto dado está relacionado con lo representado por otro punto, se unen tales puntos con un segmento de recta espacial. Siempre habrá posibilidad de ordenar los puntos de modo tal que no se crucen sus segmentos de unión entre sí.
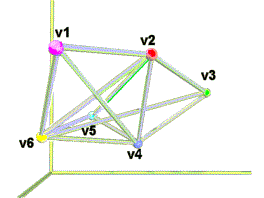
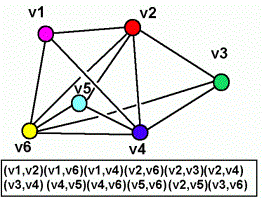
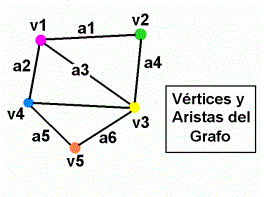
 Se ilustran ( fig.1 y fig. 2 ) tanto  la configuración espacial tomando a las esferitas como puntos y a las barras como segmentos, como la representación planar de relaciones, junto a su enumeración.
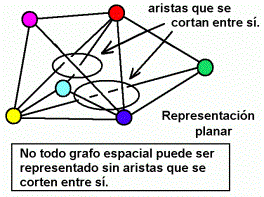
 La primera cuestión a tratar aquí sería la de considerar la posibilidad de que por este último modo de representar el grafo, se obtenga un esquema de segmentos de unión de modo tal que no se corten entre sí. (fig.3)
 Puede probarse que siempre existirán grafos que no puedan dibujarse de modo tal que ninguna de sus aristas o segmentos de unión se corten entre sí.
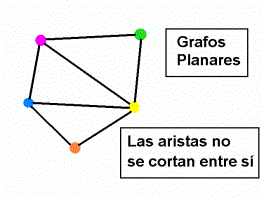
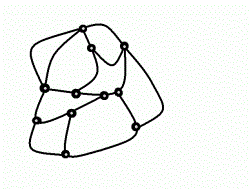
 Pero en el caso que ninguna arista se corta mutuamente con otra, estaremos en presencia de un grafo denominado planar. (fig.4)
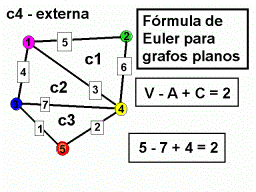
En las siguientes ilustraciones se indican tanto los elementos constitutivos de un grafo planar (fig.5). Seguidamente se indica (fig.6) la fórmula de Euler para grafos planares, que relaciona vértices, aristas y caras de un grafo planar, notando que se llama cara a la superficie plana limitada por un ciclo de aristas del grafo, incluso la exterior al grafo.
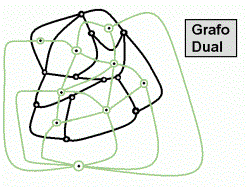
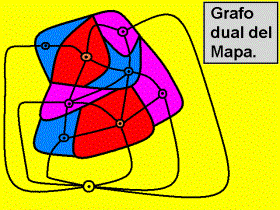
Dado un grafo planar, se puede obtener otro grafo planar uniendo entre sí a puntos únicos elegidos para cada cara, de modo tal que haya una nueva arista cruzando cada arista del grafo original, a este grafo planar se lo denomina grafo dual del original(fig.7y8).
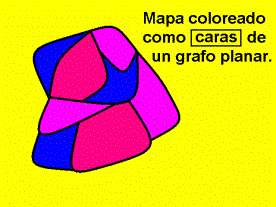
 Dado un grafo planar, si coloreamos cada una de sus caras obtenemos lo que se da en llamar un mapa (fig.9), y tal mapa tiene claramente asociado un grafo dual planar (fig.10).
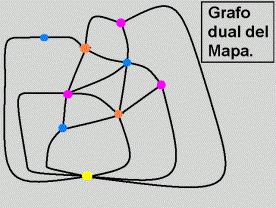
Aquí (fig.11) se lo ilustra de otro modo, notando que cada vértice hereda el color de la región de la que provino en el grafo original.
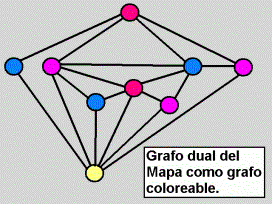
 Un grafo se llama coloreable cuando todo vértice vecino, a través de alguna arista, tiene un color distinto, o de otro modo, vértices vecinos tienen diferente color (fig.12).
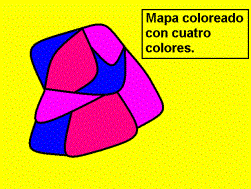
Se ha demostrado en la década de los '70 que cualquier mapa puede bien colorearse con a lo sumo 4 colores (fig.13). Se agrega "bien colorearse" dado que no siempre se comienza coloreando bien y se traba el coloreado con sólo cuatro colores, debiendo comenzar de nuevo de otro modo.
Según lo visto inmediatamente arriba, esto quiere decir que todo grafo planar es grafo coloreable con cuatro colores, ya que puede ser el dual de otro grafo plano.
 Que  pueda cualquier grafo colorearse con cuatro colores no significa que no haya casos en que se lo pueda hacer con menos colores, como en el caso del mapa producido por la partición del plano por medio de rectas tiradas al azar, caso en el que alcanza, como se evidencia, con sólo dos colores(fig.14).