MÁQUINAS DE ENGRANAJES
Máquinas de Engranajes.(I)

Máquinas de Engranajes.(I)

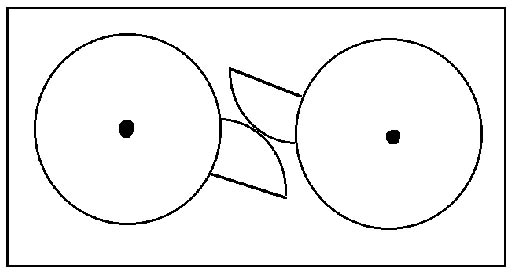
| 1)Breve descripción del Modelo- Se trata de dos
juegos de engranajes dentados de formas elíptica y oval tetralobulada.
La construcción del óvalo lobulado se hace de acuerdo con
Artobolevski (autor del tratado monumental de mecanismos (Ed. MIR Moscú)
Se observa que a una rotación uniforme de un engranaje, su pareja
responde de modo variable. Estas curvas cerradas son unos de los pocos
ejemplos de rotación dentada entre curvas iguales.
2)Conceptos Matemáticos en juego- coordenadas polares, derivada angular, longitud de arco, pendiente polar. 3)Guía de Uso Específica del Modelo- Qué y Cómo hay que mover o realizar: Se hacen girar no muy velozmente. Qué hay que observar: La inconstancia del giro de respuesta del otro engranaje al hacer girar uniformremente el manipulado. Qué precauciónes se deben tener: No hacerlos girar muy velozmente, si se trabasen no esforzarlos. 4)Breves referencias teórico-técnicas- Para que rueden recíprocamente estas curvas deben cumplir la condición de tener para cada movimiento dado igualdad de longitudes de arco, para que no haya rozamiento, que no permitiría dentar sus contornos. |
Plantillas computacionales de curvas
Máquinas de Engranajes(II).
Maquetas de estudio de formas base y de perfiles de
dientes.
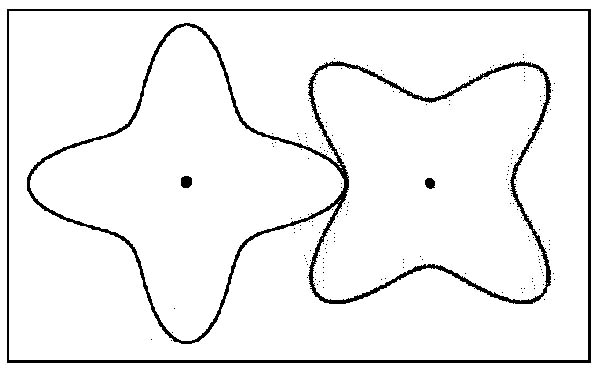
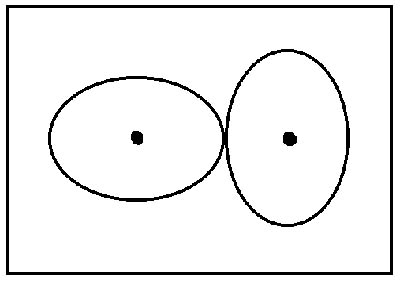
| 1)Breve descripción de los Modelos- Formas-Se
trata de juegos de curvas cerradas con formas de espirales logarítmicas
y ovales. La construcción del óvalo lobulado se hace de acuerdo
con Artobolevski (autor del tratado monumental de mecanismos (Ed. MIR Moscú).
Se observa que a una rotación de un engranaje, su pareja responde
manteniendo el contacto sin rozamiento, por lo que podrían dentarse
para construir engranajes correspondientes. Estas curvas cerradas son unos
de los pocos ejemplos de rotación dentada entre curvas iguales.
Dientes- Se muestran los perfiles planos de dientes de engranajes de evolventes de círculos y de epicicloide-hipocicloide.La propiedad es la de mantener continuamente la igualdad o proporción de ángulos de giro respectivos a cada curva base. 2)Conceptos Matemáticos en juego- coordenadas polares derivada angular longitud de arco pendiente polar 3)Guía de Uso Específica del Modelo- Qué y Cómo hay que mover o realizar: Se hacen girar ambas piezas de cada juego manteniéndolas en contacto (tienen contornos de goma). Qué hay que observar: En las formas-Que ruedan una sobre la otra sin resbalar. En los dientes:Que se cumple la igualdad de ángulos de giro. Qué precauciónes se deben tener:Tratar delicadamente los modelos pues son de material débil. 4)Breves referencias teórico-técnicas- En las formas-Para que rueden recíprocamente estas curvas deben cumplir la condición de tener para cada movimiento dado igualdad de longitudes de arco, para que no haya rozamiento, que no permitiría dentar sus contornos. Plantilla computacional de curva con segmentos de espiral logarítmica. |
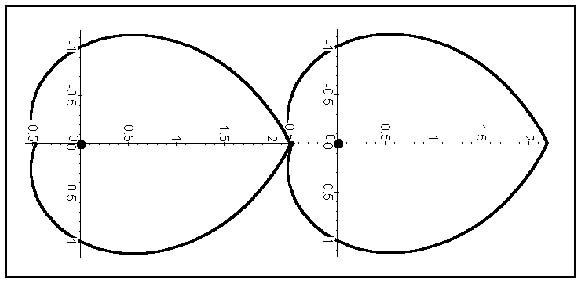
| En los dientes-El perfil de los dientes obedece a la evolvente del círculo base, consiguiéndose de este modo mantener la igualdad o la proporción de ángulos de rotación. |