![[Maple Bitmap]](images/curnu1.gif)
ARCHIVOS TEÓRICOS DEL MUSEO MATEMÁTICO.
ÁREA- ANÁLISIS-
TEMA-SUPERFICIES MÍNIMAS Y CON CURVATURA PRESCRIPTA.
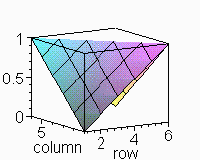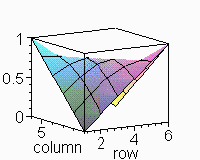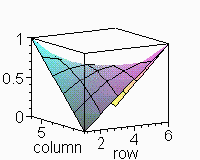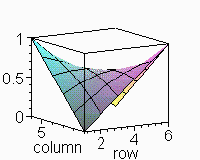
//////Superficie de curvatura media prescripta
nula en dominio de contorno cuadrado de lado L , partido en n partes////////////
Autor- Leonard Echagüe-Mate UBA Museum- lechague@dm.uba.ar
Dado un dominio cuadrado con valores predeterminados
de la función en su contorno, nulos en el caso plano y
de altura de un tetraedro en el caso de Schwarz, a partir
de una reticulación del dominio, se expresan las formulas
de las derivadas en función de los valores de las funciones
en los puntos de la malla reticular, luego de lo cual se procede,
mediante un algoritmo de gradiente descendente ,a encontrar
discretamente los valores de la funcion que cumplen con la
ecuación diferencial.
OBSERVAR LAS COINCIDENCIAS CON LO OBTENIDO EN
LOS OTROS ARCHIVOS DEL TEMA SUPERFICIES MÍNIMAS.
LAS ANIMACIONES DEL WORKSHEET ESTÁN ACTIVAS.
EN WORKSHEET COMPRIMIDO SE MUESTRAN LOS RESULTADOS PARCIALES
Gradiente descendente -caso plano -
Aquí se trabaja con gradiente descendente
ACTIVAR ANTES Planteo
ojo con el alpha no puede ser mayor que el centesimo
>
>
> desvio:=0;
![[Maple Math]](images/curnu12.gif){kind=small}
> for i from 1 by 1 to n-1 do
> for j from 1 by 1 to n-1 do
> desvio:=desvio+(poli[i,j])^2;
>
> od;od;
> print(desvio);
////////////////////////////////////////////
> gradesvio:=array(1..n-1,1..n-1,[]);
![[Maple Math]](images/curnu13.gif){kind=small}
> for i from 1 by 1 to n-1 do
> for j from 1 by 1 to n-1 do
> gradesvio[i,j]:=diff(desvio,h[i,j]);
> od:od:
> evalm(convert(gradesvio,matrix)):
> gradesvio[1,1];
> with(plots):
>
caso plano
> h1:=array(1..n-1,1..n-1,[]);
![[Maple Math]](images/curnu14.gif){kind=small}
> h:=array(0..5,0..5,[[1,1,1,1,1,1],[1,1,2,3,1,1],[1,-1,1,1,2,1],[1,2,1,1,4,1],[1,1,2,3,1,1],[1,1,1,1,1,1]]):
> evalm(convert(h,matrix));
![[Maple Math]](images/curnu15.gif)
> h[0,0];
![[Maple Math]](images/curnu16.gif){kind=small}
>
> print(evalf(desvio));
![[Maple Math]](images/curnu17.gif){kind=small}
> evalm(evalf(convert(gradesvio,matrix)));
![[Maple Math]](images/curnu18.gif)
> alpha:=0.006;
![[Maple Math]](images/curnu19.gif){kind=small}
>
>
> for k from 1 by 1 to 100 do
> for i from 1 by 1 to n-1 do
> for j from 1 by 1 to n-1 do
> h1[i,j]:=evalf(h[i,j]-alpha*gradesvio[i,j]);
> od:od:
> for i from 1 by 1 to n-1 do
> for j from 1 by 1 to n-1 do
> h[i,j]:=h1[i,j];
> od:od:
> print(evalf(desvio)):
> p.k:=matrixplot(convert(h,matrix)):
> od:
>
> display([seq(p.k,k=1..100)],insequence=true);
![[Maple Plot]](images/curnu20.gif)
Gradiente descendente -caso Schwarz-
Aquí se trabaja con gradiente descendente ACTIVAR ANTES Planteo
ojo con el alpha no puede ser mayor que el centesimo
![[Maple OLE 2.0 Object]](images/curnu21.gif)
> h1:=array(1..n-1,1..n-1,[]);
![[Maple Math]](images/curnu22.gif){kind=small}
> h:=array(0..5,0..5,[[0,0.2,0.4,0.6,0.8,1],[0.2,0.4,0.6,0.8,1,0.8],[0.4,0.6,0.8,1,0.8,0.6],[0.6,0.8,1,0.8,0.6,0.4],[0.8,1,0.8,0.6,0.4,0.2],[1,0.8,0.6,0.4,0.2,0]]):
> convert(h,matrix);hp:=matrixplot(convert(h,matrix)):
![[Maple Math]](images/curnu23.gif)
> print(evalf(desvio));
![[Maple Math]](images/curnu24.gif){kind=small}
> evalm(evalf(convert(gradesvio,matrix)));
![[Maple Math]](images/curnu25.gif)
> alpha:=0.009;
![[Maple Math]](images/curnu26.gif){kind=small}
>
> for k from 1 by 1 to 120 do
> for i from 1 by 1 to n-1 do
> for j from 1 by 1 to n-1 do
> h1[i,j]:=evalf(h[i,j]-alpha*gradesvio[i,j]);
> od:od:
> for i from 1 by 1 to n-1 do
> for j from 1 by 1 to n-1 do
> h[i,j]:=h1[i,j];
> od:od:
> print(evalf(desvio)):
> p.k:=matrixplot(convert(h,matrix)):
> od:
> display([hp,seq(p.k,k=1..120)],insequence=true,view=[1..6,1..6,0..1]);
