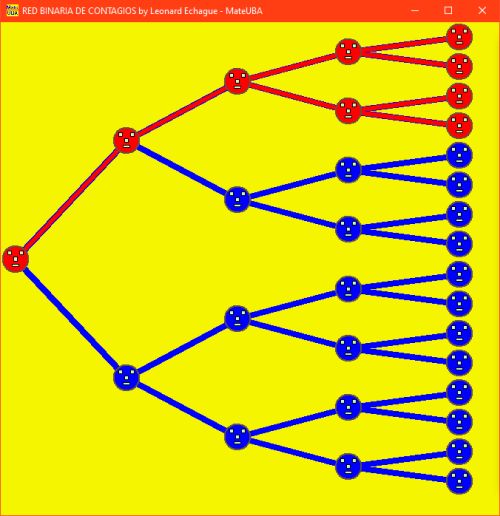
Red de contagios. Modelo simplificado.
Ideas generales y matemática subyacente
Se trata de informar sobre un tipo específico de modelo
de contagio, a través de redes simplificadas que son
grafos-árboles de grados bajos, en este caso 2 o sea
árboles binarios, es decir que se considera que cada
contagiado transmite el virus a dos personas solamente.
Se supone una situación de contagio total en la
parte inicial de una red completa partiendo de una persona,
y desarrollando el contagio hacia 4 niveles más.
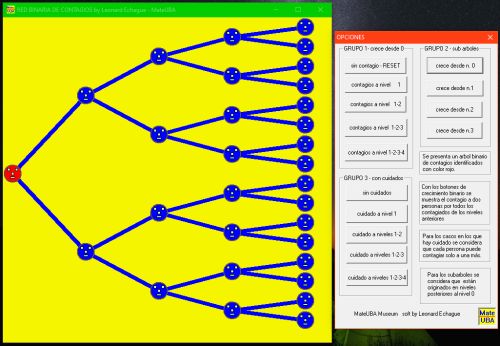
El software en entorno MSWindows (Win95->Win10)
representa visualmente al grafo binario con nodos
que corresponderían a personas que se colorean
según su estado de contagio. La interacción se
realiza por medio de una consola visual típica del
sistema de ventanas y se opera con toques de mouse.
El modelo visual interactivamente va dando cuenta de:
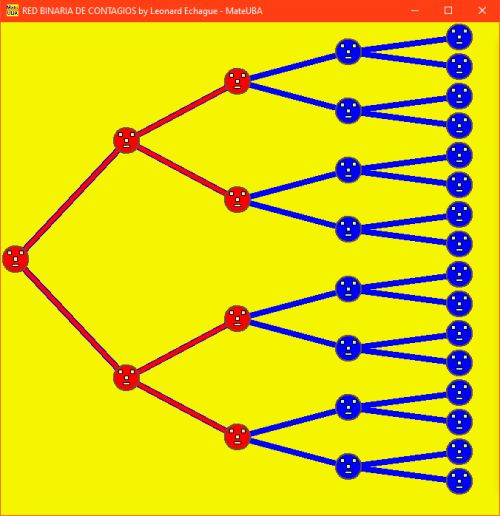
1- El crecimiento exponencial del número de contagiados
que se duplica por nivel avanzado (2,4,8,16 por nivel aislado
2,6,14 y 30 en total sin el No.1)
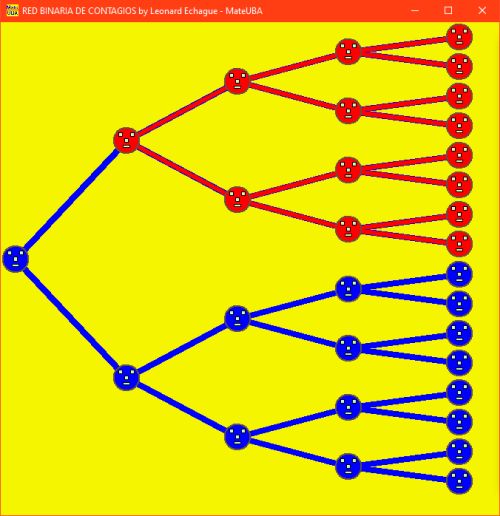
2- Si el contagiado que origina la red se hubiese aislado un poco,
en vez de contagiar a 2 personas, lo hubiera hecho con 1 persona, y si las siguientes
contagiadas no se cuidan, a pesar de ello notar que
los contagiados disminuyen a la mitad, por haberse solo cuidado
la persona que originó la red de contagios.
3- Si los sucesivos contagiados se hubiesen cuidado y solo
hubieran contagiado a 1 persona en todo nivel, notar que
el crecimiento pasa de exponencial a lineal (lo que a mediano
plazo pasa a ser constante pues los contagiados pasado
un tiempo o se curan o no están más).
4- Si el árbol comienza más tarde la cantidad de contagiados se
reduce a la mitad por cada nivel que se retrase.
El crecimiento exponencial queda claro en la interacción 1 y
se puede comparar con el lineal posible de lograr con la interacción 3.
Temas matemáticos específicos
- Grafos y crecimiento: crecimiento lineal y exponencial
-grafo simple
-grafo dirigido
-nodo (arista, lado)
-nodo antecesor
-nodo sucesor
-grado de nodo
-grado saliente de nodo
-árbol
-árbol binario
-árbol binario uniforme
-nivel
-rama
-grafos lineales (rectos) y crecimientos lineales
-arboles n-arios y crecimientos exponenciales
-factor de contagio R y árboles
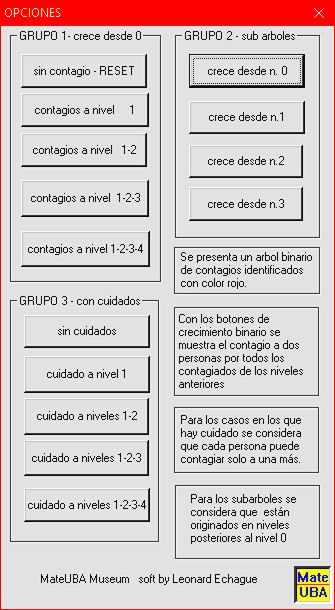
Interacciones de usuario-
Son dos tipos de desarrollo que se efectúan operando
con toques de mouse en la consola de opciones.
1- Se va completando el grafo por nivel suponiendo
el máximo número de contagios contemplado (2 por cada
persona ya contagiada).
2-3- Se considera que hay menos contagios para los
sucesivos niveles de dos maneras diferentes:
- en 2 iniciando los contagios más tardíamente
- en 3 disminuyendo a 1 los contagios por persona sucesivamente
hasta que el crecimiento de contagios se hace lineal.
La observación va indicando los tipos de
crecimiento que se van dando, y ello por las
cantidades de contagiados que pueden contarse directamente.
Observaciones sobre modelación teórica del problema
Se trata de simplificar las circunstancias
que se están modelando para que sean
comprendidas, pero que también ofrezcan
alguna información cierta. No se
obtendrán datos numéricos precisos
sino tendencias comparativas ciertas que servirán
para la orientación en el problema. Es decir que lo que
puede inferirse del funcionamiento del modelo
pueda extenderse como tendencia a otros casos más
generales, un ejemplo sería lo atinente al decrecimiento de
casos por el cuidado que disminuye los contagios por persona,
esto es válido para cualquier situación de contagio, pero
en lo mostrado aquí refiere a la red binaria simplificada.
Hipótesis del modelo
Se supone (situación muy idealizada) que los
contagios en principio son siempre de una persona a otras dos personas
Otra hipótesis implícita es sobre el tiempo (oportunidad) de los
contagios, ya que no se cumple en la relidad que se den a la vez (en el mismo instante) y por nivel de nodos, esta circunstancia no invalida las
conclusiones pues lo que aquí interesa son las
relaciones lógicas del fenómeno del contagio observadas cuando ya
cierta población se ha contagiado completamente.
Funcionamiento del modelo
Para entender sobre la situación se parte de una
población ya contagiada según cierto patrón de
contagios (patrón este muy simple), y para obtener
las simples conclusiones sobre
el comportamiento de los contagios en red
se opera de modo "inverso" ya que se trata de averiguar
"qué hubiera pasado si", es decir, modificando
condiciones hacia el pasado, esto lo que se
experimenta con las interacciones 2 y 3.
Ilustra la diferencia entre tratamientos cuantitativos y cualitativos
evaluaciones aproximadas o comparativas y de tendencias de crecimiento
Alcances y límites del modelo
-Las conclusiones sobre las disminuciones de casos al cuidarse,
ya por postergar el contagio o por disminuir la diseminación, se
extienden hacia los casos generales de contagio.
-Uniformidad ideal de contagios desde cada persona que en la realidad no se da
-Hay circunstancias que podrían invalidar al modelo
construido, un ejemplo estaría dado por la posibilidad de
reinfecciones (donde podrían haber grafos con ciclos, que entonces
descartarían a los árboles como modelo)
|