EXPERIMENTANDO
CON LAS CÓNICAS
1
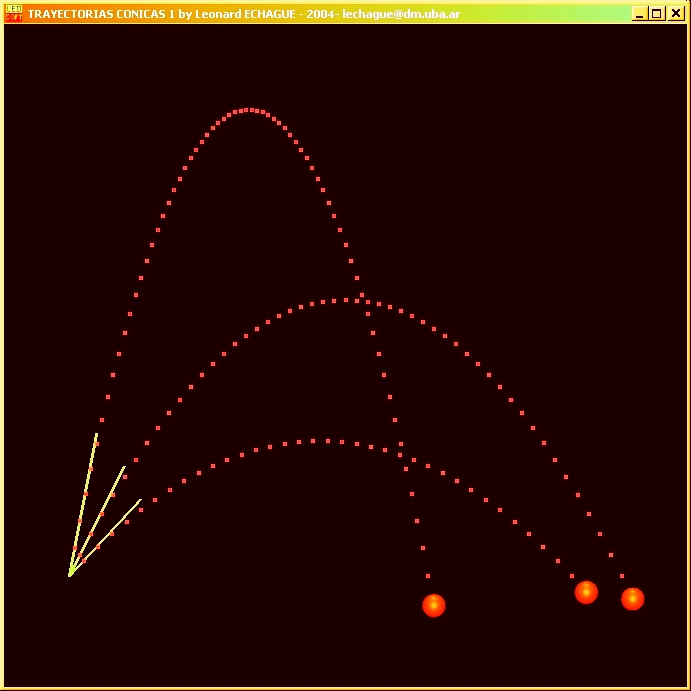
En las imágenes de estas primeras simulaciones gráficas
y computacionales se observan las trayectorias de proyectiles disparados
con velocidades iniciales indicadas por los segmentos inclinados situados
al comienzo de los recorridos de las trayectorias.
Estas simulaciones son trazadas de acuerdo al cálculo
de los valores de las ecuaciones de la cinemática de las partículas
materiales bajo un campo de gravedad constante y vertical, como puede suponerse
que existe en una pequeña parte de la superficie de la tierra.
Ya se sabe, desde hace tiempo, que si no hubiese rozamiento del
aire y tampoco otros factores perturbadores, tales trayectorias tendrían
la forma de parábolas.
Nótese que el movimiento total puede descomponerse en
dos movimientos: uno horizontal de velocidad uniforme, y otro vertical
acelerado hacia abajo como el de tirar una piedra hacia arriba verticalmente
.
2
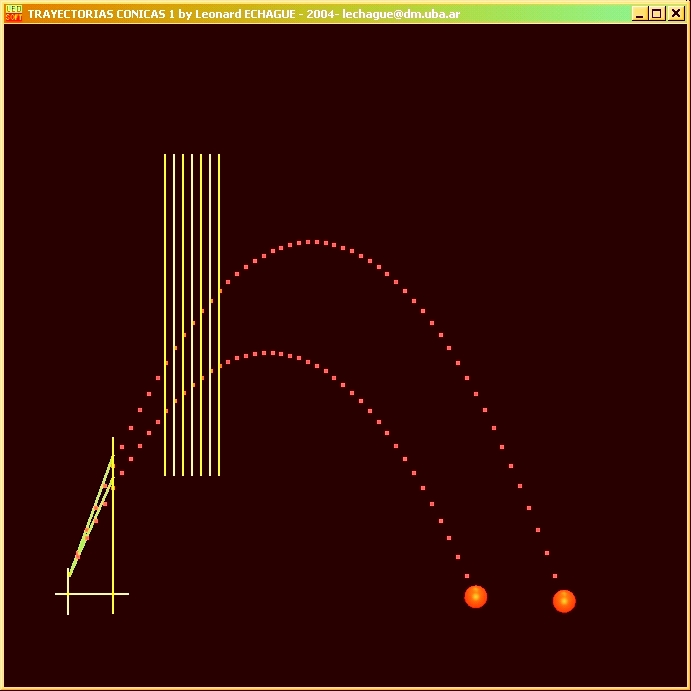
Estas segundas simulaciones se basan en la resolución numérica
de las ecuaciones de Newton de la dinámica y de la gravitación.
Se simula el comportamiento de partículas materiales móviles
bajo la acción de un campo gravitatorio central, aquí
supuestamente producido por una gran masa.
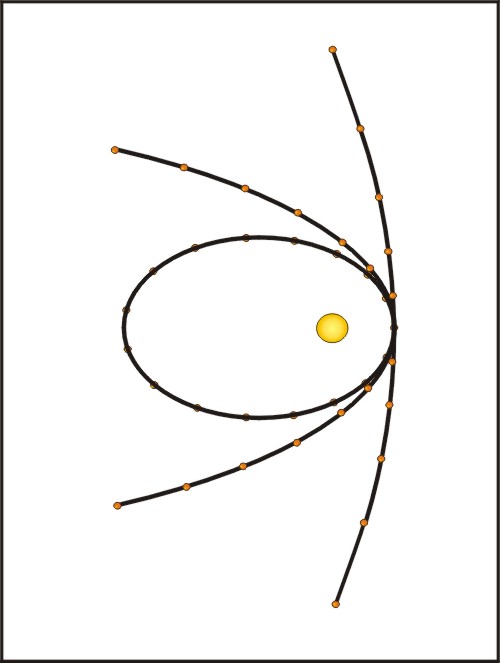
Se muestran las trayectorias de una partícula orbitando, para
diferentes valores de velocidad inicial con dirección vertical desde
cierto punto de la horizontal que pasa por la masa que atrae.
Nótese que se parte de curvas cerradas para bajas velocidades
iniciales, llegando a curvas abiertas para más altas velocidades
iniciales.
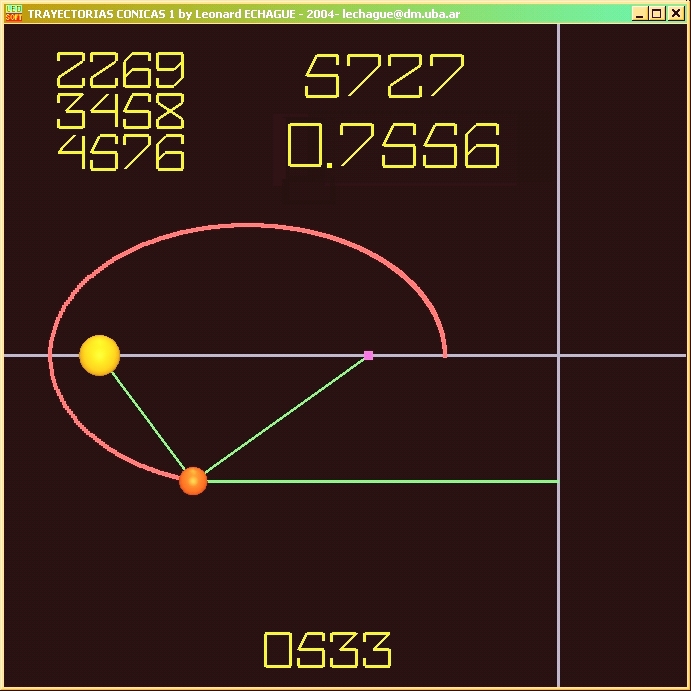
3
Las cónicas pueden ser definidas como lugares geométricos
de puntos que cumplen ciertas propiedades métricas. Aquí
se expresan las condiciones de la suma de distancias a los focos de la
elipse y de la proporción de excentricidad.
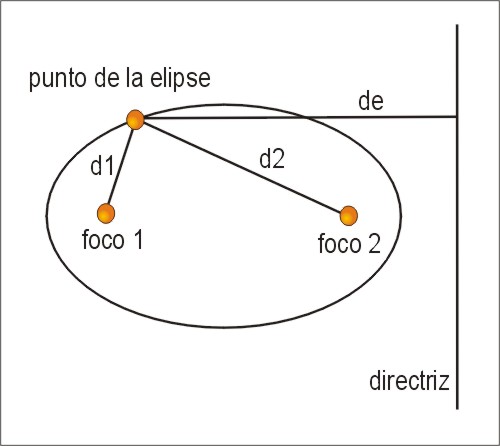
d1+d2=constante d2/de=excentricidad
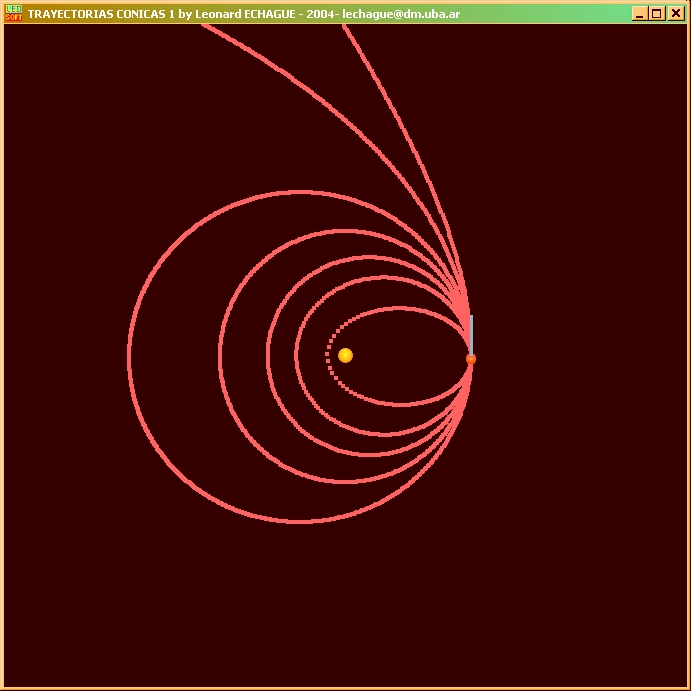
En esta tercera simulación se ilustra las verificación
aproximada de las propiedades métricas que definen a las trayectorias
de recorrido de las partículas del caso de simulación anterior
mostrando por qué pueden ser consideradas cónicas y en este
caso particular una elipse.
Se utiliza una curva de base obtenida en el punto anterior mediante
la simulación dinámica.
Esto ilustra elementalmente cómo partiendo de la
experiencia física puede obtenerse conocimiento de la geometría,
o de otro modo, cómo del cumplimiento de las leyes de la dinámica
por simulación puede obtenerse cierto conocimiento de la geometría.
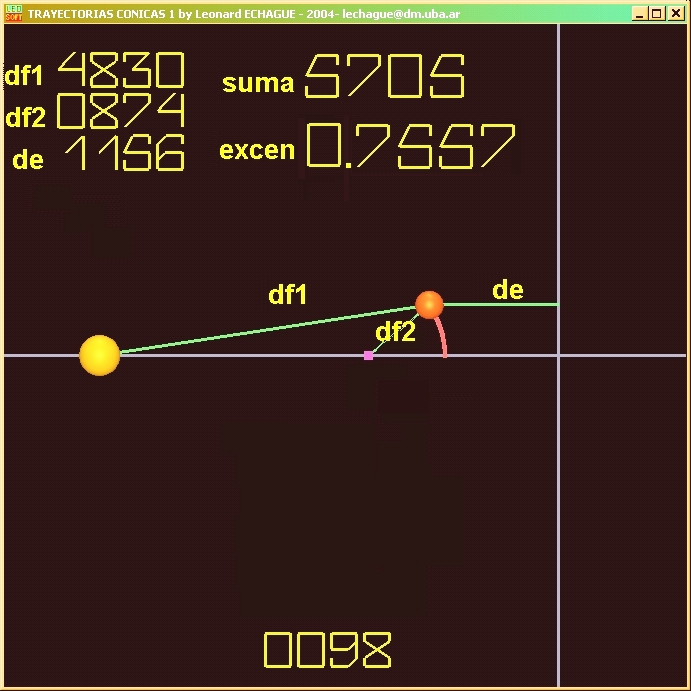
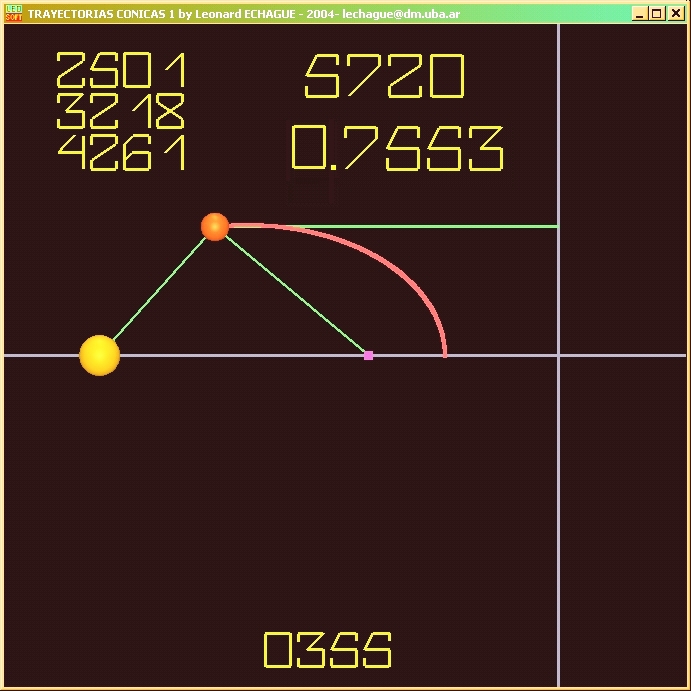
En la simulación se procede a expresar en forma entera
aproximada las distancias entre el centro de atracción y la partícula
que orbita, y entre la partícula y un eje directriz.
Para ello se ubican los focos y una directriz de una elipse,
calculando su posición según las medidas de la órbita.
Se nota que se cumple con gran aproximación tanto la ley de
la suma de las distancias, como la de la proporción de excentricidad
respecto del eje directriz.
Newton en sus Principios Matemáticos de la Filosofía
Natural demuestra teórica y precisamente que los cuerpos que describen
órbitas bajo un campo de gravedad central lo hacen sobre trayectorias
cónicas.
Notar que los errores en la suma y en la excentricidad
calculadas en la simulación son del orden menor al 1%, por
lo tanto se puede en primera aproximación considerar que la órbita
es elíptica.
4
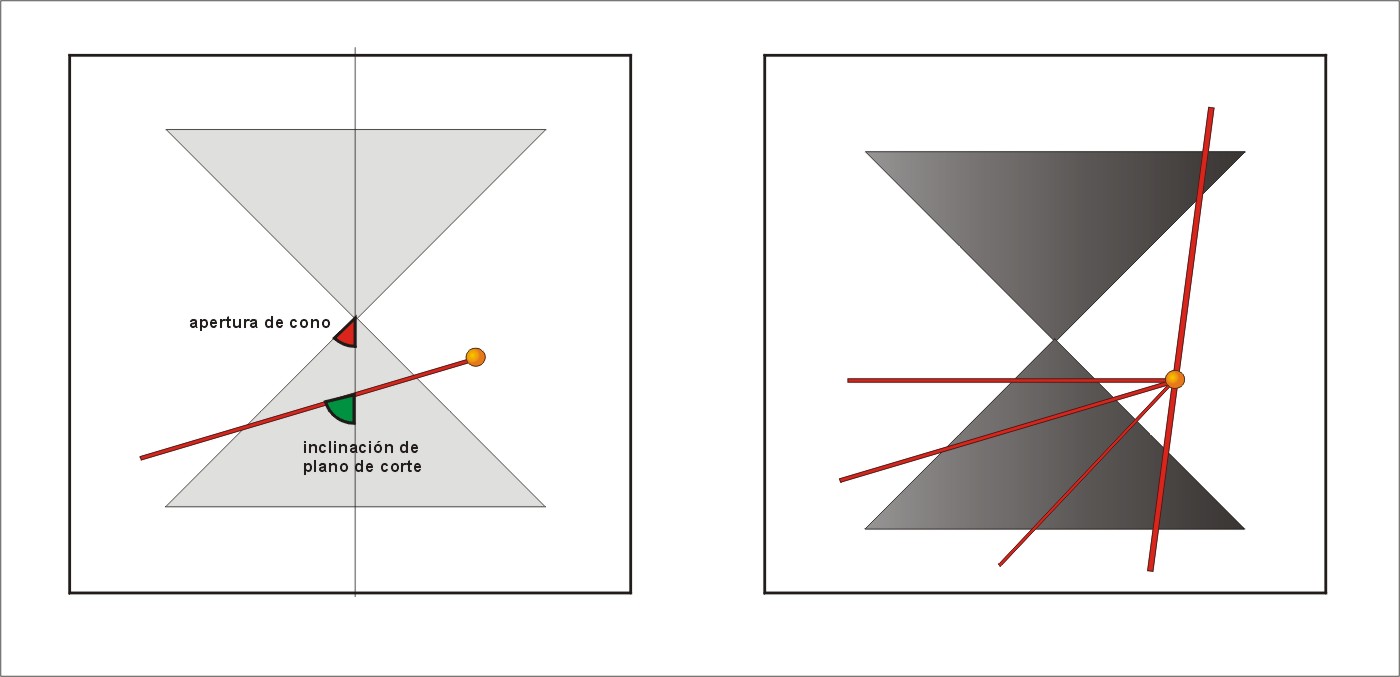
Ya en la antigüedad a Apolonio trató con el problema de
las cónicas consideradas como trazas de cortes de conos por planos.
Pueden clasificarse las cónicas según los ángulos
de inclinación de los planos de corte respecto de la apertura del
cono que están cortando.
Cuando el ángulo de corte es mayor que el ángulo
de apertura del cono la curva que se traza es una elipse. Y podría
agregarse que la excentricidad está entre cero y uno.
Cuando el ángulo de corte es igual que el ángulo
de apertura del cono la curva que se traza es una parábola.
Y podría agregarse que la excentricidad es uno.
Cuando el ángulo de corte es menor que el ángulo
de apertura del cono la curva que se traza es una hipérbola.
Y podría agregarse que la excentricidad es mayor que uno.
Nótese que el plano de corte en el caso de las hipérbolas
corta al cono en sus dos partes, la superior y la inferior, obteniéndose
de este modo las dos ramas.
En las imágenes de los gráficos computacionales
siguientes se observan diferentes posiciones de los planos que cortan solamente
a la parte inferior del cono.
5
En las primeras tres imágenes se observa que el plano corta
al cono a través de una elipse.
En tres imágenes centrales se observa que el plano
corta al cono a través de una parábola.
En las últimas tres imágenes se observa que el plano
corta al cono a través de una hipérbola.
6
Un matemático llamado Dandelin construyó una configuración
geométrica que fácilmente demuestra que el corte de un cono
por un plano es una curva cónica. Aquí se toma un caso
muy especial de cono, que es el cilindro, y que sería como un cono
con el vértice en el infinito. Con el auxilio de dos esferas
tangentes, tanto al cilindro como al plano de corte, se obtienen fórmulas
de las que se deduce la propiedad del lugar geométrico de la elipse,
es decir, la suma de las distancias desde cada punto de la elipse de corte
a dos puntos fijos sobre el plano de corte es constante. El truco
principal para esta demostración geométrica es el de percatarse
de la igualdad de las longitudes de ambos segmentos de recta extendidos
entre un punto exterior a una esfera y sus sendos puntos de
tangencia sobre esa esfera. Nótese que aunque se cambie el punto
elegido de la elipse para realizar la construcción de Dandelin,
se sigue cumpliendo el esquema de cálculo de las distancias.
7
Recapitulando lo visto:
Las cónicas aparecen como formas geométricas que describen
algunas de las posibles trayectorias de cuerpos libres en el espacio
al moverse interactuando recíprocamente.
Para demostrar esto precisamente, se utilizan las formulaciones de
la dinámica para determinar la geometría, como lo hizo
Isaac Newton en los Principia.
Pero ilustrativamente pueden simularse computacionalmente los comportamientos
de las partículas, haciendo que la computadora resuelva en cada
paso numéricamente las ecuaciones del movimiento y de la atracción
gravitatoria de los cuerpos, verificándose aproximadamente la validez
de la consideración realizada.
Ya desde la antigüedad se estudiaron a las cónicas como
las curvas engendradas por los cortes de conos por planos, y mediante programas
computacionales gráficos pueden verse algunos casos.
Y se termina uniendo ambos modos de considerar a las cónicas,
tanto como trazas de corte que como conjuntos de puntos del plano que cumplen
una propiedad geométrica, y esto se ilustra mediante la construcción
de Dandelin.
Faltaría agregar que ciertamente hay relación entre la
velocidad inicial de la partícula bajo acción de un campo
gravitatorio central y la excentricidad de la cónica generada como
trayectoria, pero de modo somero puede decirse que a partir de cierto valor
de velocidad inicial, la excentricidad aumenta cuando la velocidad inicial
aumenta. Y por esto, si la velocidad inicial es muy elevada se tienen trayectorias
hiperbólicas, y al ir disminuyendola se pasa por una trayectoria
parabólica, llegándose luego a trayectorias elípticas.
Leonard Echague- MateUBA Museum - FCEN - UBA
|