Mathematical Objects
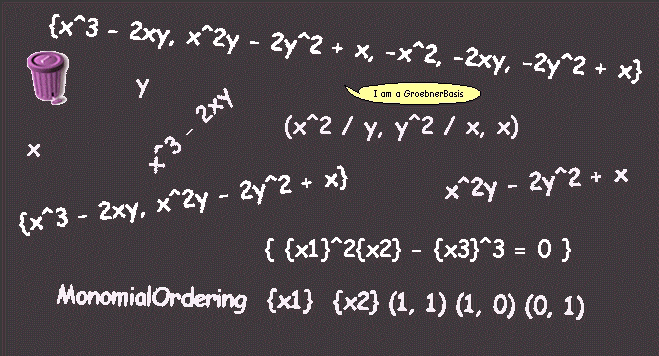
Mathematical Objects
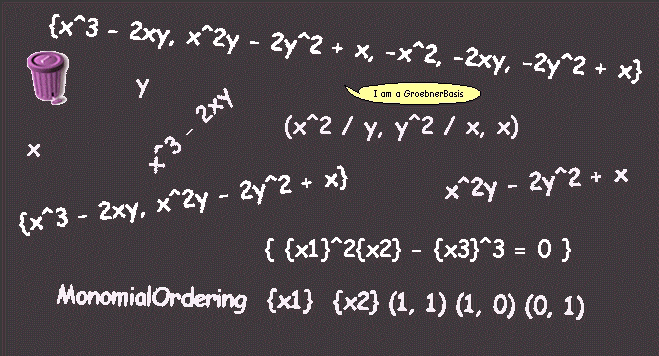
This is the change set of this work.
The object of this project is to solve the Implicitation Problem, i.e. given an algebraic variety described by a rational parametric equation, find a system of polynomial equations which define it in implicit form.
We created classes to model multivariate polynomials: MonomialLiteral, Monomial y Polynomial. MonomialLiteral models the literal part of the monomials, i.e., products of indeterminate powers. The Monomials know a coefficient and a literal. Finally, each Polynomial represets a polynomial and stores the collection of not null monomials (Monomials). We put the polynomial division algorithms in different classes: PolynomialDivisor (one variable), PolynomialPseudoDivisor (one or many variables, but w.r.t. a variable), MultiPolynomialDivisor (many variables with fixed monomial ordering). We also have objects which are rational functions; we created the RationalFunction class, this class knows a numerator and a denominator.
![]()
Class
Ideal
You can create ideals from a generating set
Class protocol
instance creation
generator: anIdealGenerator
Also, we can ask an ideal for a generating set accessing generators The ideals allow arithmetic operations
Instance protocol
arithmetic
* anIdeal
+ anIdeal
You can compare ideals trought inclusions
comparing
<= anIdeal
= anIdeal
And we can inquire whether an ideal is null or includes an element
testing
includes: anObject
isNull
Private protocol
accessing-private
generators:
![]()
This class models polinomial ideals over the rationals using Groebner basis.
Class
IdealWithGroebner
You can create an IdealWithGroebner giving a Groebner basis
Class protocol
instance creation
groebnerBasis: aGroebnerBasis
They can answer a Groebner basis and they can solve the Ideal Membership Problem
Instance protocol
accessing
groebner
testing
includes: aPolynomial
![]()
This class models an oredered set of generators.
Class
IdealGenerator
You can add an element to the set, get the n-th element and get the size of the set.
acessing
add: anObject
size
at: anInteger
There are also enumerating messages
enumerating
do: aBlock
collect: aBlock
select: aBlock
You can test the inclusion
testing
includes: anObject
![]()
Class
GroebnerBasis
We can create new Groebner bases from a generating set and a monomial ordering or with a default (lexicographic) ordering.
Class protocol
instance creation
from: anIdealGenerator ordering: aMonomialOrdering
from: anIdealGenerator
The Groebner bases can tell the ordering they are using. Furthermore, a basis can be asked for the remainder of the division of a polynomial by the basis, and given a Groebner basis, you can get a minimal one generating the same ideal
Instance protocol
accessing
ordering
remainderOf: aPolynomial
minimal
A Groebner basis can say whether it is minimal or reduced
testing
isMinimal
isReduced
![]()
If you want to know the impelmentation, open a browser on the code. Anyway, the following diagram can give you some idea(ls) of the implementation we prefer
Object
MonomialLiteral (contents)
Monomial (literal coefficient)
Polynomial (monomials)
MonomialOrdering (indeterminates weighs)
PolynomialDivisor (dividend divisor quotient remainder done)
PseudoPolynomialDivisor (dividend divisor indeterminate quotient remainder done)
MultiPolynomialDivisor (dividend divisor ordering quotients remainder done)
RationalFunction (numerator denominator)
Ideal (generators)
IdealWithGroebner (groebner)
IdealGenerator (contents)
GroebnerBasis (ordering)
PolynomialEquation (polynomial)
PolynomialSystem (equations)
RationalParametrization (contents)
AlgebraicVariety (system parametrization)
Here, we are going to see how we can create polynomials. First, we create the indeterminates
x
y
¬ Polynomial y.Then, we see how is the polynomial ordering we are going to use (a general explanation of monomial orderings is in the class comment of MonomialOrdering)
grlex
MonomialOrdering {x1} {x2} (1, 1) (1, 0) (0, 1)
And then, our polynomials f1 and f2
f1
{x1}^3 - 2{x1}{x2}
f2
¬ x**2*y - (2*y*y) + x.{x1}^2{x2} - 2{x2}^2 + {x1}
Now, we wish the ideal generating by these polynomials f1 and f2
basis
{{x1}^3 - 2{x1}{x2}, {x1}^2{x2} - 2{x2}^2 + {x1}}
and calculate the Groebner basis
GroebnerBasis from: basis ordering: grlex
{{x1}^3 - 2{x1}{x2}, {x1}^2{x2} - 2{x2}^2 + {x1}, -{x1}^2, -2{x1}{x2}, -2{x2}^2 + {x1}}
Finally, we create a rational parametrization
param
param add: x squared / y; add: y squared / x; add: x; yourself
({x1}^2 / {x2}, {x2}^2 / {x1}, {x1})
and calculate the implicit form
param implicit
{ {x1}^2{x2} - {x3}^3 = 0 }
![]() Adele Goldberg, David Robson, "Smalltalk-80: The Language", Addison-Wesley, 1986.
Adele Goldberg, David Robson, "Smalltalk-80: The Language", Addison-Wesley, 1986.
![]() Cox, Little, Oshea, "Ideals, Varieties and Algorithms", Springer-Verlag, 19 .
Cox, Little, Oshea, "Ideals, Varieties and Algorithms", Springer-Verlag, 19 .
![]() B. Mishra, "Algorithmic Algebra", Springer-Verlag, 19 .
B. Mishra, "Algorithmic Algebra", Springer-Verlag, 19 .
![]() Enzo R. Gentile, "Anillo de polinomios", Editorial Docencia, 1980.
Enzo R. Gentile, "Anillo de polinomios", Editorial Docencia, 1980.
You can download the change set clicking here.
Comments to:
Luciano Notarfrancesco
lnotarfr@dc.uba.arPablo Malavolta
volta@ce.fcen.uba.ar
![]()