Linear Algebra project
|
The aim of this project is to construct all mathematical objects
found in Linear Algebra without lossing generality.
We use AlgebraicAmbients to keep definitions independent from the field of scalars and LinearAmbients to be able to define "abstract" linear spaces and perform operations on them as tensor product, hom, dual, direct sum, etc. and any combination of them. Also we don't want to restrict ourselves to the case where all indexes occurring in bases, coordinates and matrixes are 1, 2, ..., n. Some times these objects are canonically indexed by an arbitrary set I. That's why we have IndexedTuples and IndexedMatrixes. |
Download the last change set
Linear.zip [Dec-31-1998]
We are currently considering the following problem:
If V is a linear space with scalars in a field K acting on the left (suppose that K is not commutative), then the dual V* is a right K-linear space (but not a left K-linear space). So, in order to face this "side change", each LinearSpace should have the knowledge of whether the scalar action is from the left or the right.
Algebraic Ambients
Suppose you want to implement Linear Algebra in Squeak (that's what we are doing). The first object you need is the tuple. OK. When you consider the class Tuple you want instance creation messages for the canonical vectors ei. But when mathematicians say ei they are assuming we all know the value of n. In other words, they are speaking about ei,n. But, what is even more problematic, they are assuming we all know the field of scalars. So, our instance creation method should look like this
e: i dim: n scalars: scalarsArguments i and n are clear. But, what about scalars? We cannot use the SmallInteger objects 1 and 0 for the unit and the zero elements inside ei, because this is not general enough. We want our Linear Albebra construction to be valid for any field K.
One could say: well, let's model the class Field. Yes, but that is not easy and goes beyond our current problem. Up to now, all we need for tuples is to speak about 1 and 0 with generality.
The solution we decided was to create the class AlgebraicAmbient. An AlgebraicAmbient is an object that can respond a unit and a zero. It represents a prime field or ring (the intersection of many rings). Since zero equals unit - unit, these object only must remember the unit as an instance variable.
Also, the class AlgebraicAmbient knows the collection of all available ambients. So, when you say
AlgebraicAmbient withUnit: anObjectthe answer is a previously created ambient with that unit, or a new created instance.
The initialization of the class creates the "default" instance withUnit: 1 (the SmallInteger). But once you create, say, IntegerMod5, you can add a new ambient
AlgebraicAmbient withUnit: (1 mod: 5)Overview
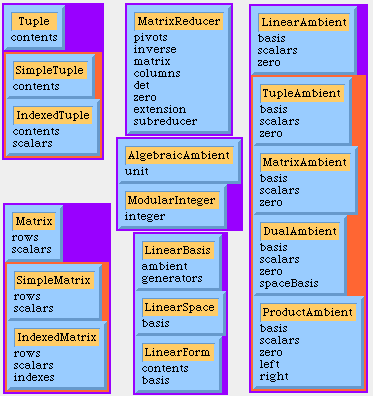
Tuple
SimpleTuple
IndexedTuple
Tuple
Abstract class. You could hang your particular subclass here.
SimpleTuple
The instances are normal tuples of some dimension $n$ as (-1, 2, 0), etc.
IndexedTuple
The instances are families with free indexes $(a_i)_{i \in I}$
Matrix
SimpleMatrix
IndexedMatrix
Matrix
Abstrac class. You could hang your particular subclass here.
SimpleMatrix
The instances are normal matrices of some dimension $n \times m$, as
$\pmatrix{1 & -1 \cr 0 & 1\cr}$.
IndexedMatrix
Matrices with index in a Cartesian product: $(a_{ij})_{(i,j) \in I\times J}$
AlgebraicAmbient
ModularInteger
AlgebraicAmbient
Each instance is a prime field or ring. Examples: rationals, Zp, algebraic
numbers, Q[i], etc. This class allows us to implement all other classes
without loss of generality in the choice of the field (or ring) of scalars.
Instance variables named 'scalars' as in LinearBasis, LinearAmbient,
IndexedTuple or SimpleMatrix refer to AlgebraicAmbients.
ModularInteger
Abstract class. Each concrete subclass is created on demand. For example
evaluating (2 mod: 5) for the first time creates the subclass IntegerMod5.
You can create Zp as an AlgebraicAmbient sending the following message:
- AlgebraicAmbient withUnit: (1 mod: 5)
CartesianProduct
OrderedPair
OrderedPair
A generalization of Point. Each pair may contain any object in the x and y
coordinates.
CartesianProduct
A special kind of set (or collection) whose elements are OrderedPairs.
LinearBasis
LinearAmbient
TupleAmbient
MatrixAmbient
ProductAmbient
DualAmbient
LinearBasis
The instances are linear base of some linear space with free indexes.
LinearAmbient
Root of a hierarchy of ambients modeling different vector spaces where all
subspaces finally live. You should hang here new kinds of linear ambients.
The main responsibility of a LinearAmbient is to keep a cannon basis and to
respond the coordinates of any vector in that basis. LinearAmbients will
free us the tedious task of worry about coordinates.
TupleAmbient
An important an very simple example of linear ambient. You can create an
instance providing the dimension of the ambient and specifying scalars or
indexes as desired.
MatrixAmbient
Another important and very simple example modeling spaces where the elements
are matrices.
ProductAmbient
If you have two ambients, you can form the product (direct sum) using this
class.
TensorAmbient [coming soon]
If you have two linear spaces, you can form the tensor product.
DualAmbient
If you have a linear space V, you can consider the dual V* as an ambient by
itself.
HomAmbient [coming soon]
If you have two linear spaces V and W, the Hom(V,W) is an ambient
MatrixReducer
EuclideanReducer
MatrixReducer
The instances are algorithms reducing (triangulating) matrices with
coefficients in a field. You create a MatrixReducer sending it the message
- MatrixReducer input: aMatrix
EuclideanReducer [coming soon]
This reducer is used when you have not a field but and Euclidean ring of
scalars (Z, k[x], etc).
Linear Ambients
When you think about Tuples, Matrixes, LinearForms, LinearEquations, etc. sooner or later you encounter two kind of objects: subspaces and bases. A (linear) subspace has a basis and you want to express each vector of the subspace as a linear combination of the basis.Consider an example. You have Q3 (being Q the rationals). In this space you have a subspace L, say the plane defined by
x + y + z = 0.You find a basis for L, say B={(1, -1, 0), (1, 0, -1)}. Now you want to find the coordinates of a vector v=(a, b, c) in L in terms of the basis B. You can use the following algorithm:
- Put the elements of B as columns of a Matrix new
- Put the element v as the third column
- Reduce the matrix using elementary operations on the rows
- Read the coordinates in the third column
| 1 | 1 | a |
| -1 | 0 | b |
| 0 | -1 | c |
| 1 | 1 | a |
| 0 | 1 | a+b |
| 0 | -1 | c |
| 1 | 0 | -b |
| 0 | 1 | a+b |
| 0 | 0 | a+b+c |
and since a+b+c=0, we obtain
[v]B = (-b, a+b) "coordinates of v in basis B"
You can use another algorithm. But no matter what algorithm you employ, the point is that all algorithms need to know a crucial information: how to write the coordinates of all involved vectors as tuples. In other words, each time we want to calculate the coordinates of a vector v in some basis B, we must first be able to express the coordinates of the elements of B and v in terms of another basis.
A similar situation arises when you want to express a number in some basis. For example, you need to express the number 14 in decimal in order to convert it to binary 2r1110.
The problem seems to be circular: to be able to find the coordinates we must first find the coordinates. Fortunately, it isn't.
In our example above, we wanted the coordinates of v in the basis {v1, v2}. But what we needed were the coordinates of v1, v2 and v in the canonical basis of Q3 (not in the basis B of L). And there is an important difference between Q3 and L: Q3 has a canonical basis (while L hasn't).
Note that the notion of 'canonical' is not mathematically definied. Still a canonical basis has an intuitive property: it makes it easy to find the coordinates of any vector.
Examples of canonical basis are:
- Tuples: e1=(1, 0, 0, ...), e2=(0, 1, 0, ...), e3=(0, 0, 1, ...), ...
- Matrices: e11, e12, e13, ..., eij. Where eij is the matrix having 1 at i@j and zero anywhere
- Polynomials: 1, x, x2, x3, ...
- Polynomials: 1, x, y, z, x2, xy, xz, y2, yz, z2, ....
When we have a canonical basis we know how to compute the coordinates of a vector. So we should capture this concept and keep it in mind because this is the clue to work with abstract linear bases.
By thinking in canonic bases we realize that they appear tied to linear ambients. By linear ambient I mean a linear space that's the mother of all subspaces in a given problem. Examples of linear ambients are
Q2, Q3, Zpn, k[x], k[x]n, k[x, y], knxm, ...A linear ambient (feel free to suggest another name) is not a subspace, it is the space. What I'm trying to say is that we have linear spaces and subspaces, the spaces are the ambients where all vectors live.
My claim is that each linear ambient has a canonic basis. Understanding that "canonic" means that we have no problem to compute the coordinates of a given vector, no matter what the vector is.
In fact, I'm saying more. I'm saying that a linear ambient is a place where we have a canonic baisis. To put it clearer, we could define the class
LinearAmbient ('basis')where we have two instance methods:
LinearAmbient | coordinatesOf: vectorand
LinearAmbient | verctorWithCoordiantes: aTupleThese methods are inverses each other. Of course, the class LinearAmbient is abstract and the implementantion of those methods is a subclass responsibility. Filling up the code for these two methods exactly corresponds to the fact that this task is supposed to be easy when we have a canonic basis.
Thus, LinearAmbient is a framework helping us to define concrete ambients. Some examples follow.
TupleAmbient (a number n is given)
Canonic basis: e1,
e2, ...,
en
TupleAmbient | coordinatesOf: vector
^vector
TupleAmbient | verctorWithCoordiantes: aTuple
^aTuple
MatrixAmbient (n and m are given)
Canonic basis: eij,
(i runing from 1 to: n;
j runing from 1 to: m)
MatrixAmbient | coordiantesOf: matrix
^Tuple
dim: n * m
fromBlock:
[:k | matrix at: (k - 1 // m)
+ 1 @ (k - 1 \\ m) + 1]
MatrixAmbient | verctorWithCoordiantes: aTuple
^Matrix
dim: n * m
fromBlock:
[:ij | aTuple at: (ij x - 1) * m + ij y]
DualAmbient (a subspace V of dim n
with a basis is given)
Canonic basis: the dual basis of the given basis of V
DualAmbient | coordinatesOf: form
^Tuple
dim: n
fromBlock: [:k | form at: (basis at: k)]
DualAmbient | verctorWithCoordiantes: aTuple
sum := (self canonic: 1) * (aTuple at: 1).
2 to: n
do: [:k | sum := (self canonic: k) * (aTuple at: k) + sum].
^sum
Following these ideas it is easy to implement TensorAmbient, HomAmbient, ProductAmbient, PolynomialAmbient, etc. Note that with a few classes we could capture all relevant ambients to work with and combine them in any way (using tensor product, hom, direct sum, dual, etc.). Then once we have the ambients we could easily consider "abstract" subspaces living inside them. Doing that we ensure ourselves that all abstract concepts can be modeled and all algorithms will work.